已知数列{an}的首项a1=5,前n项和为Sn,
且Sn+1=2Sn+n+5(n∈N*).
(Ⅰ)证明数列{an+1}是等比数列;
(Ⅱ)令f(x)=a1x+a2x2+…+anxn,求函数f(x)在点x=1处的导数f'(1).
解:(Ⅰ)由已知S
n+1=2S
n+n+5,∴n≥2时,S
n=2S
n-1+n+4,
两式相减,得S
n+1-S
n=2(S
n-S
n-1)+1,
即a
n+1=2a
n+1,从而a
n+1+1=2(a
n+1).
当n=1时,S
2=2S
1+1+5,∴a
1+a
2=2a
1+6又a
1=5,∴a
2=11,
从而a
2+1=2(a
1+1).故总有a
n+1+1=2(a
n+1),n∈N*.
又∵a
1=5,,∴a
n+1≠0,从而
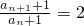
.
即{a
n+1}是以a
1+1=6为首项,2为公比的等比数列.
(Ⅱ)由(Ⅰ)知a
n=3×2
n-1.
∵f(x)=a
1x+a
2x
2+…+a
nx
n∴f'(x)=a
1+2a
2x+…+na
nx
n-1.
从而f'(1)=a
1+2a
2+…+na
n=(3×2-1)+2(3×2
2-1)+…+n(3×2
n-1)
=3(2+2×2
2+…+n×2
n)-(1+2+…+n)
=
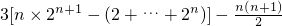
=
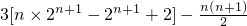
=
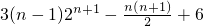
.
分析:(Ⅰ)先根据S
n+1=2S
n+n+5可得到S
n=2S
n-1+n+4,然后两式相减可得到S
n+1-S
n=2(S
n-S
n-1)+1,即a
n+1=2a
n+1然后两边同时加1即可得到a
n+1+1=2(a
n+1),即
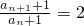
.从而得证.
(Ⅱ)先根据(Ⅰ)求出a
n的通项公式,再对函数f(x)进行求导,得到f'(x)的表达式,然后将a
n的表达式代入进行分组求和即可.
点评:本题主要考查等比数列的证明、求导运算和数列的分组求和.考查基础知识的综合运用和计算能力.

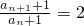 .
.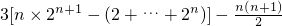
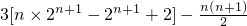
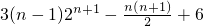 .
.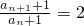 .从而得证.
.从而得证.
