
分析 方法一:利用三角形的面积相等,求得圆心与半径,即可求得圆方程,设P(1+cosθ,1+sinθ),由正弦函数的性质即可求得u的最大值及相应的P点坐标.
方法二:由题意可得内切圆的方程为(x-1)2+(y-1)2=1,可得3x2+3y2-6x-6y+3=0,整体代入|PA|2+|PB|2+|PO|2=-2y+22,由函数的思想可得最值.
解答 解:方法一:设△OAB内切圆的圆心为(a,a)
∵0(0,0),A(3,0),B(0,4),
∴|OA|=3,|OB|=4,|AB|=5,
由等面积可得$\frac{1}{2}$×3×4=$\frac{1}{2}$(3+4+5)a,解得a=1
∴△OAB内切圆的圆心为(1,1),半径为1,
∴△OAB内切圆方程为(x-1)2+(y-1)2=1;
设P(1+cosθ,1+sinθ),
则u=(1+cosθ)2+(1+sinθ)2+(1+cosθ-3)2+(1+sinθ)2+(1+cosθ)2+(1+sinθ-4)2…(6分)
即u=20-2sinθ,θ∈R…(8分)
故当且仅当sinθ=-1时,umax=22…(10分)
∴umax=22,相应的点为P(1,0)…(12分)
方法二:设△OAB内切圆的圆心为(a,a)
∵0(0,0),A(3,0),B(0,4),
∴|OA|=3,|OB|=4,|AB|=5,
由等面积可得$\frac{1}{2}$×3×4=$\frac{1}{2}$(3+4+5)a,解得a=1
∴△OAB内切圆的圆心为(1,1),半径为1,
∴△OAB内切圆方程为(x-1)2+(y-1)2=1;
∵点P是△ABO内切圆上一点,设P(x,y)
则(x-1)2+(y-1)2=1,
∴x2+y2-2x-2y+1=0,
∴3x2+3y2-6x-6y+3=0,
∴u=|PA|2+|PB|2+|PO|2=(x-3)2+y2+x2+(y-4)2+x2+y2,
=3x2+3y2-6x-8y+25=3x2+3y2-6x-6y+3-2y+22=-2y+22
∴|PA|2+|PB|2+|PC|2=-2y+22,(0≤y≤2),
∴y=0时上式取最大值22,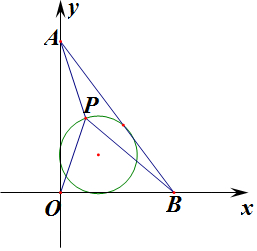
点评 本题考查三角形内切圆的求法,圆的参数方程,两点之间的距离公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
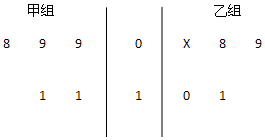 如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示
如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
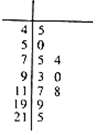 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com