
(14分)已知等比数列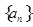 的前
的前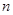 项和为
项和为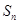 ,且
,且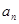 是
是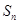 与2的等差中项,
与2的等差中项,
等差数列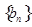 中,
中,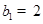 ,点
,点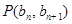 在直线
在直线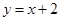 上.
上.
⑴求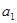 和
和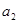 的值;
的值;
⑵求数列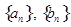 的通项
的通项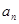 和
和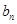 ;
;
⑶ 设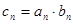 ,求数列
,求数列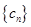 的前n项和
的前n项和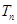 .
.
(1)a2=4 ; (2bn=2n-1; (3)Tn=(2n-3)2n+1+6
【解析】本试题主要是考查了等差数列的通项公式的求解哦数列求和的综合运用。
(1) an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
进而得到第二项的值。对于又Sn—Sn-1=an,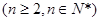
∴an=2an-2an-1∴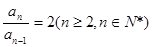 ,即数列{an}是等比数据列
,即数列{an}是等比数据列
以及∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0得到数列的通项公式。
(2)由上可知,cn=(2n-1)2n
利用错位相减法可知得到数列的和的求解。
解:(1)∵an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
a1+a2=S2=2a2-2,解得a2=4 ……3分
(2)∵Sn=2an-2,Sn-1=2an-1-2,
又Sn—Sn-1=an,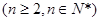
∴an=2an-2an-1,
∵an≠0,
∴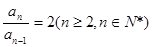 ,即数列{an}是等比树立∵a1=2,∴an=2n
,即数列{an}是等比树立∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1, ……8分
(3)∵cn=(2n-1)2n
∴Tn=a1b1+ a2b2+····anbn=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
因此:-Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn=(2n-3)2n+1+6 ……14分


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考文数 题型:解答题
(本题13分)
已知等比数列 的前
的前 项和是
项和是 ,满足
,满足 .
.
(Ⅰ)求数列 的通项
的通项 及前
及前 项和
项和 ;
;
(Ⅱ)若 数列
数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅲ)若对任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市毕业班第四次调研测试文科数学试卷(解析版) 题型:选择题
已知等比数列 的前
的前 项和为
项和为 ,且满足
,且满足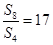 ,则公比
,则公比 =(
)
=(
)
A. B.
B.  C. 2
D.
C. 2
D. 
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三上学期期始考试理科数学试卷(解析版) 题型:解答题
已知等比数列 的前
的前 项和为
项和为 ,正数数列
,正数数列 的首项为
的首项为 ,
,
且满足: .记数列
.记数列 前
前 项和为
项和为 .
.
(Ⅰ)求 的值; (Ⅱ)求数列
的值; (Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)是否存在正整数 ,且
,且 ,使得
,使得 成等比数列?若存在,求出
成等比数列?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届广东省度高二下学期期中文科数学试卷(解析版) 题型:选择题
已知等比数列{ }的前
}的前 项和为
项和为 ,且
,且 ,则数列
,则数列 的公比
的公比 的值为( )
的值为( )
A. 2 B. 3 C. 2或-3 D. 2或3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com