
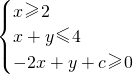 ,目标函数z=3x+y的最小值为5,则该目标函数z=3x+y的最大值为
,目标函数z=3x+y的最小值为5,则该目标函数z=3x+y的最大值为 的可行域,根据目标函数的解析式形式,分析取得最优解的点的坐标,然后根据分析列出一个含参数的方程组,消参后即可得到c的取值,然后求出此目标函数的最大值即可.
的可行域,根据目标函数的解析式形式,分析取得最优解的点的坐标,然后根据分析列出一个含参数的方程组,消参后即可得到c的取值,然后求出此目标函数的最大值即可.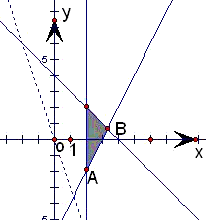 解:画出x,y满足的可行域如下图:
解:画出x,y满足的可行域如下图: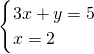 得A(2,-1)
得A(2,-1) 得B(3,1)
得B(3,1)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com