
【题目】已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求函数a的取值范围;
(2)记函数![]() 的两个极值点为
的两个极值点为![]() ,
,![]() ,且
,且![]() ,证明对任意实数
,证明对任意实数![]() ,都有不等式
,都有不等式![]() 成立.
成立.
【答案】(1)![]() (2)证明见详解.
(2)证明见详解.
【解析】
(1)将函数有两个极值点的问题,转化为导函数有两个零点的问题,再转化为函数图像有交点的问题,利用导数的几何意义求得临界状态时直线的斜率即可求得参数范围;
(2)根据![]() 的单调性,将问题转化为求证
的单调性,将问题转化为求证![]() ,再构造函数
,再构造函数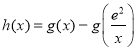 ,根据其单调性,即可证明.
,根据其单调性,即可证明.
(1)依题![]()
![]()
![]() 有两个不同的极值点,即
有两个不同的极值点,即![]() 有两个不等实根.
有两个不等实根.
亦即函数![]() 与
与![]() 图象在
图象在![]() 上有两个不同交点
上有两个不同交点
若令过原点且与![]() 图象相切的直线斜率为k,则只需
图象相切的直线斜率为k,则只需![]()
设切点为![]() ,则
,则![]() ,而
,而![]()
故![]() ,于是
,于是![]() ,所以
,所以![]()
(2)证明:令![]() 则
则![]()
由![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
知![]() 是
是![]() 的极大值点
的极大值点
故![]() 且
且![]()
![]() 等价于
等价于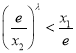
∵![]() ,
,![]() ∴
∴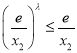
故只需证![]() 即可
即可
令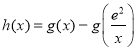 ,
,![]()
则![]()
故![]()
∵![]() ∴
∴![]() ,
,![]() ,∴
,∴![]()
∴![]() 在
在![]() 单调递增∴
单调递增∴![]()
∴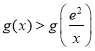 ∵
∵![]() ∴
∴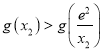
又∵![]() ∴
∴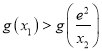
又∵![]() ,
,![]() 且
且![]() 在
在![]() 单调递增
单调递增
∴![]() ∴
∴![]() 即原不等式成立
即原不等式成立


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2019年暑假期间,河南有一新开发的景区在各大媒体循环播放广告,观众甲首次看到该景区的广告后,不来此景区的概率为![]() ,从第二次看到广告起,若前一次不来此景区,则这次来此景区的概率是
,从第二次看到广告起,若前一次不来此景区,则这次来此景区的概率是![]() ,若前一次来此景区,则这次来此景区的概率是
,若前一次来此景区,则这次来此景区的概率是![]() .记观众甲第n次看到广告后不来此景区的概率为
.记观众甲第n次看到广告后不来此景区的概率为![]() ,若当
,若当![]() 时,
时,![]() 恒成立,则M的最小值为__________.
恒成立,则M的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 恒过
恒过![]() 的一个焦点
的一个焦点![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的顶点均在
的顶点均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直线
,若直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,求直线
,求直线![]() 与
与![]() 轴交点的坐标.
轴交点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 首项和公差都是
首项和公差都是![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,等比数列
,等比数列![]() 各项均为正数,公比为q,记
各项均为正数,公比为q,记![]() 的前n项和为
的前n项和为![]() :
:
(1)写出![]()
![]() 构成的集合A;
构成的集合A;
(2)若将![]() 中的整数项按从小到大的顺序构成数列
中的整数项按从小到大的顺序构成数列![]() ,求
,求![]() 的一个通项公式;
的一个通项公式;
(3)若q为正整数,问是否存在大于1的正整数k,使得![]()
![]() 同时为(1)中集合A的元素?若存在,写出所有符合条件的
同时为(1)中集合A的元素?若存在,写出所有符合条件的![]() 的通项公式,若不存在,请说明理由.
的通项公式,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前n项和.
的前n项和.
(1)求![]() 和
和![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(2)设![]() .
.
①若![]() ,求k的值;
,求k的值;
②求证:数列(![]() 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第![]() 条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第
条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第![]() 条规定:对不礼让行人的驾驶员处以扣
条规定:对不礼让行人的驾驶员处以扣![]() 分,罚款
分,罚款![]() 元的处罚.下表是某市一主干路口监控设备所抓拍的
元的处罚.下表是某市一主干路口监控设备所抓拍的![]() 个月内驾驶员不“礼让斑马线”行为统计数据:
个月内驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
不“礼让斑马线”驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求不“礼让斑马线”驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该路口
,并预测该路口![]() 月份的不“礼让斑马线”驾驶员人数;
月份的不“礼让斑马线”驾驶员人数;
(2)若从表中![]() 月份和
月份和![]() 月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为
月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为![]() 的样本,再从这
的样本,再从这![]() 人中任选
人中任选![]() 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: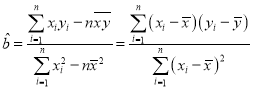 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在2016年的“减员增效”中对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的![]() 领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得![]() 元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年
元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年![]() 元,分流后进入新经济实体,第
元,分流后进入新经济实体,第![]() 年的收入为
年的收入为![]() 元;
元;
(1)求![]() 的通项公式;
的通项公式;
(2)当![]() 时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com