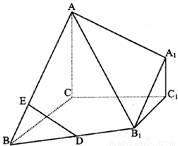
分析:(Ⅰ)过D作DF⊥BC于点F(或取BC的四等分点)先证明平面EFD∥平面ACC
1A
1,从而得ED∥平面ACC
1A
1.
(Ⅱ)由(Ⅰ)过F作FG⊥BA于G,连GD证明∠FGD=θ,在Rt△DFG中解得tgθ=2
.
(Ⅲ)由V
C-ABB1=V
A-CBB1 解得C到平面ABB
1的距离为
.
解答:
解:(Ⅰ)过D作DF⊥BC于点F(或取BC的四等分点),所以FD∥C
1C,
所以C
1C∥平面ACC
1A
1.
又因为E为AB上一点,且BE=
BA,
所以EF∥AC,
所以EF平面ACC
1A
1.
所以平面EFD∥平面ACC
1A
1,
又因为ED?平面EFD,
所以ED∥平面ACC
1A
1(4分).
(Ⅱ)由(Ⅰ)过F作FG⊥BA于G,连GD,
由题意可得:FD⊥平面ABC,
所以AB⊥平面FDG,
所以GD⊥AB,
所以可得∠FGD=θ,
因为E为AB上一点,且BE=
BA,
所以点F为线段BC的四等分点,
所以
FD=.
因为D为BB
1中点,所以DF=
C
1C=
AC.
所以在Rt△DFG中,解得tgθ=
=2
(4分)
(Ⅲ)由题意可得:V
A--CBB1=
×S△CB1B×C1C =.
因为AC=2,所以AB=2
,B
1B=
,AB
1=3,
所以由正弦定理与余弦定理可得:S
△AB1B=3.
由V
C-ABB1=V
A--CBB1可得:C到平面ABB
1的距离为
.(4分)
点评:本题考查用线面平行的判定定理证明线面平行,以及求二面角的平面角,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,以及考查利用等体积法求点到平面的距离.

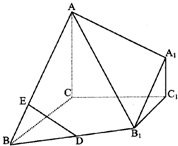 如图,在三棱台ABC-A1B1C1中,CA,CB,CC1两两垂直且长度相等,B1C1=
如图,在三棱台ABC-A1B1C1中,CA,CB,CC1两两垂直且长度相等,B1C1= 解:(Ⅰ)过D作DF⊥BC于点F(或取BC的四等分点),所以FD∥C1C,
解:(Ⅰ)过D作DF⊥BC于点F(或取BC的四等分点),所以FD∥C1C,

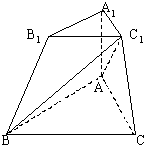 如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.
如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a. 如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.
如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.
 BC,D为BB1中点,E为AB上一点,且BE=
BC,D为BB1中点,E为AB上一点,且BE= BA,
BA,