
【题目】已知函数f(x)=kex﹣x3+2 (k∈R)恰有三个极值点xl,x2,x3,且xl<x2<x3.
(I)求k的取值范围:
(II)求f(x2)的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)求出函数的导数,整理得![]() ,令
,令![]() ,根据函数的单调性进行求解;(Ⅱ)求出函数的导数,求出
,根据函数的单调性进行求解;(Ⅱ)求出函数的导数,求出![]() 的解析式,根据函数的单调性求出
的解析式,根据函数的单调性求出![]() 的范围即可.
的范围即可.
试题解析:(Ⅰ)f'(x)=kex﹣3x2.
由题知方程kex﹣3x2=0恰有三个实数根,
整理得![]() .…
.…
令![]() ,则
,则![]() ,
,
由g'(x)>0解得0<x<2,由g'(x)<0解得x>2或x<0,
∴g(x)在(0,2)上单调递增,在(﹣∞,0),(2,+∞)上单调递减.…
于是当x=0时,g(x)取得极小值g(0)=0,
当x=2时,g(x)取得极大值![]() . …
. …
且当x→﹣∞时,g(x)→+∞;当x→+∞时,g(x)→0,
∴![]() .…
.…
(Ⅱ)由题意,f'(x)=kex﹣3x2=0的三个根为x1,x2,x3,且x1<x2<x3,
∴0<x2<2,且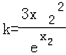 ,…
,…
∴![]() ,…
,…
令μ(x)=﹣x3+3x2+2(0<x<2),
则μ'(x)=﹣3x2+6x=﹣3x(x﹣2),
当0<x<2时,μ'(x)>0,即μ(x)在(0,2)单调递增,…
∴f(x2)∈(2,6). …


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两位同学8次数学单元测试的成绩构成如下所示的茎叶图,且甲同学成绩的平均数比乙同学成绩的平均数小2.
(1)求m的值以及乙同学成绩的方差;
(2)若数学测试的成绩高于85分(含85分),则视为优秀.现对乙同学的成绩进行深入分析,在乙同学的优秀成绩中任取2次成绩,求至少有一次抽取的成绩超过90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为了让高一学生更有效率地利用周六的时间,在高一新生第一次摸底考试后采取周六到校自主学习,同时由班主任老师值班,家长轮流值班.一个月后进行了第一次月考,高一数学教研组通过系统抽样抽取了![]() 名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:

(1)请画出这次调查得到的![]() 列联表;并判定能否在犯错误概率不超过
列联表;并判定能否在犯错误概率不超过![]() 的前提下认为周六到校自习对提高学生成绩有效?
的前提下认为周六到校自习对提高学生成绩有效?
(2)从这组学生摸底考试中数学优良成绩中和第一次月考的数学非优良成绩中,按分层抽样随机抽取![]() 个成绩,再从这
个成绩,再从这![]() 个成绩中随机抽取
个成绩中随机抽取![]() 个,求这
个,求这![]() 个成绩来自同一次考试的概率.
个成绩来自同一次考试的概率.
下面是临界值表供参考:

(参考公式: 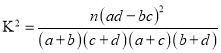 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个推理中,属于演绎推理的是( )
A. 观察下列各式:72=49,73=343,74=2401,…,则72015的末两位数字为43
B. 观察![]() ,可得偶函数的导函数为奇函数
,可得偶函数的导函数为奇函数
C. 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积之比为1:8
D. 已知碱金属都能与水发生还原反应,钠为碱金属,所以钠能与水发生反应
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点P到定点F(0,1)的距离比它到直线![]() 的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
(Ⅰ)求曲线C的方程;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求△ABM的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com