在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ 的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ 中应用了( )A．分析法B．综合法C．分析法和综合法综合使用D．间接证法题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

在证明命题“对于任意角θ,cos⁴θ-sin⁴θ=cos2θ”的过程:“cos⁴θ-sin⁴θ=(cos²θ+sin²θ)·(cos²θ-sin²θ)=cos²θ-sin²θ=cos2θ”中应用了(　　)

A．分析法

B．综合法

C．分析法和综合法综合使用

D．间接证法

从已知条件出发,推出要证的结论,满足综合法.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：不详 题型：解答题

用反证法证明：如果x>

，那么x²＋2x－1≠0.

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

下面是一段演绎推理：如果直线平行于平面，则这条直线平行于平面内的所有直线；已知直线b∥平面α，直线a?平面α；所以直线b∥直线a，在这个推理中（　　）

A．大前提正确，结论错误

B．小前提与结论都是错误的

C．大、小前提正确，只有结论错误

D．大前提错误，结论错误

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：
①

，这与三角形内角和为

相矛盾，

不成立；②所以一个三角形中不能有两个直角；③假设三角形的三个内角

、

中有两个直角，不妨设

；正确顺序的序号为 ( )

A．①②③

B．③①②

C．①③②

D．②③①

查看答案和解析>>

科目：高中数学 来源：不详 题型：填空题

－2

与

－

的大小关系是______________．

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

用反证法证明命题“三角形的内角中至少有一个角不大于

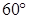”时，反设正确的是

A．假设三个内角都不大于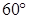	B．假设三个内角都大于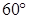
C．假设三个内角至多有一个大于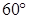	D．假设三个内角至多有二个大于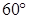

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

求证：(1)