Question

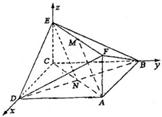
 (本题满分15分) 如图，已知正方形和矩形所在的平面互相垂直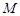，，，是线段的中点.

（Ⅰ）求证：//平面；

（Ⅱ）求二面角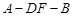的大小；

（Ⅲ）试在线段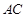上确定一点，使得与所成的角是.

 

Answer 1

【答案】

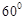（Ⅰ）见解析；（Ⅱ）60º。（Ⅲ）点P是AC的中点。

【解析】本题考查直线与平面平行，二面角的知识，考查空间想象能力，逻辑思维能力，是中档题。

（1）要证AM∥平面BDE，直线证明直线AM平行平面BDE内的直线OE即可，也可以利用空间直角坐标系，求出向量AM ，在平面BDE内求出向量 NE ，证明二者共线，说明AM∥平面BDE，

（2）在平面AFD中过A作AS⊥DF于S，连接BS，说明∠BSA是二面角A-DF-B的平面角，然后求二面角A-DF-B的大小；也可以建立空间直角坐标系，求出

NE • DB =0， NE • NF =0说明 NE 是平面DFB的法向量，求出平面DAF的法向量 AB =(- 2 ，0，0)，然后利用数量积求解即可．

（3）点P是AC的中点时，满足PF和CD所成的角是60º，运用向量的方法证明。

解: (Ⅰ)记AC与BD的交点为O,连接OE,   ∵O、M分别是AC、EF的中点，ACEF是矩形，∴四边形AOEM是平行四边形，∴AM∥OE。∵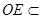平面BDE， 平面BDE，

∴AM∥平面BDE。

(Ⅱ)在平面AFD中过A作AS⊥DF于S，连结BS，∵AB⊥AF， AB⊥AD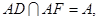， ∴AB⊥平面ADF，∴AS是BS在平面ADF上的射影，由三垂线定理得BS⊥DF。∴∠BSA是二面角A—DF—B的平面角。

在RtΔASB中，∴

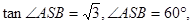
∴二面角A—DF—B的大小为60º。

（Ⅲ）设CP=t（0≤t≤2）,作PQ⊥AB于Q，则PQ∥AD，

∵PQ⊥AB，PQ⊥AF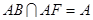，，∴PQ⊥平面ABF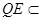，平面ABF，∴PQ⊥QF。

在RtΔPQF中，∠FPQ=60º，PF=2PQ。∵ΔPAQ为等腰直角三角形，∴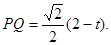

又∵ΔPAF为直角三角形，∴，∴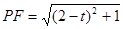

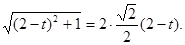
所以t=1或t=3(舍去)即点P是AC的中点。

方法二

（Ⅰ）建立如图所示的空间直角坐标系。

设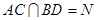，连接NE，则点N、E的坐标分别是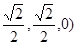（、（0,0,1）,    ∴NE=(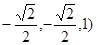,    又点A、M的坐标分别是  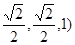（）、（  ∴ AM=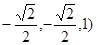（∴NE=AM且NE与AM不共线，∴NE∥AM。

又∵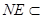平面BDE， 平面BDE，∴AM∥平面BDF。

（Ⅱ）∵AF⊥AB，AB⊥AD，AF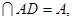∴AB⊥平面ADF。∴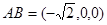为平面DAF的法向量。∵NE·DB=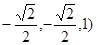（·=0，∴NE·NF=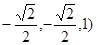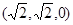（·=0得NE⊥DB，NE⊥NF，∴NE为平面BDF的法向量。∴cos<AB,NE>=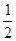∴AB与NE的夹角是60º。即所求二面角A—DF—B的大小是60º。

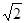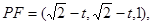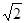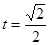（Ⅲ）设P(t,t,0)(0≤t≤)得∴CD=（，0，0）又∵PF和CD所成的角是60º。∴解得或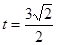（舍去），即点P是AC的中点。