
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若不等式Ax+By+5<0表示的平面区域不包括点(2,4),且k=A+2B,则k的取值范围是( )
(A)k≥- (B)k≤-
(B)k≤-
(C)k>- (D)k<-
(D)k<-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷(解析版) 题型:解答题
2×2矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(1)求矩阵M.
(2)设直线l在矩阵M对应的变换作用下得到了直线m:x-y=4.求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
在曲线C1: (θ为参数,0≤θ<2π)上求一点,使它到直线C2:
(θ为参数,0≤θ<2π)上求一点,使它到直线C2: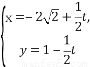 (t为参数)的距离最小,并求出该点坐标和最小距离.
(t为参数)的距离最小,并求出该点坐标和最小距离.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷(解析版) 题型:解答题
若曲线C:x2+4xy+2y2=1在矩阵M=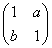 对应的线性变换作用下变成曲线C':x2-2y2=1.
对应的线性变换作用下变成曲线C':x2-2y2=1.
(1)求a,b的值.
(2)求M的逆矩阵M-1.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合计 | 80 | 1 |
若将频率视为概率,回答下列问题:
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
若随机变量ξ的分布列为:P(ξ=m)= ,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的2×2列联表:
| 男 | 女 | 总计 |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由χ2= 算得,
算得,
χ2= ≈7.8.
≈7.8.
以下结论正确的是( )
(A)有99%以上的把握认为“选择过马路的方式与性别有关”
(B)有99%以上的把握认为“选择过马路的方式与性别无关”
(C)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
(D)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数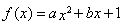 在
在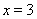 处的切线方程为
处的切线方程为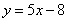 .
.
(1)求函数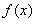 的解析式;
的解析式;
(2)若关于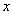 的方程
的方程 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数 的值;
的值;
(3)数列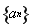 满足
满足 ,
,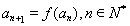 ,求
,求 的整数部分.
的整数部分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com