
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为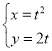 (t为参数),直线
(t为参数),直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,以坐标原点O为极点,x轴正半轴为极轴,取相同的单位长度建立极坐标系.
,以坐标原点O为极点,x轴正半轴为极轴,取相同的单位长度建立极坐标系.
(1)写出曲线C的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)若直线l与曲线C交于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=(![]() )1﹣x,则
)1﹣x,则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
⑤当x∈(3,4)时,f(x)=(![]() )x﹣3.
)x﹣3.
其中所有正确命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
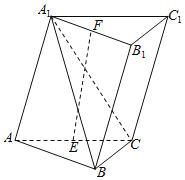
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}满足a1=1,a2=1,an+2=an+an+1,则称数列{an}为斐波那契数列,斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例.作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个圆心角为90°的扇形,连起来的弧线就是斐波那契螺旋线,如图所示的7个正方形的边长分别为a1,a2,…,a7,在长方形ABCD内任取一点,则该点不在任何一个扇形内的概率为( )
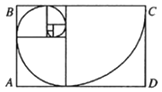
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)若a=1.解不等式f(x)≤x2﹣1;
(2)若a>0,b>0,c>0.且f(x)的最小值为4﹣b﹣c.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M:![]() 1(a>b>0)的长轴长为2
1(a>b>0)的长轴长为2![]() ,离心率为
,离心率为![]() ,过点(0,1)的直线l与M交于A,B两点,且
,过点(0,1)的直线l与M交于A,B两点,且![]() .
.
(1)求M的方程;
(2)求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点是坐标原点的抛物线![]() 的焦点
的焦点![]() 在
在![]() 轴正半轴上,圆心在直线
轴正半轴上,圆心在直线![]() 上的圆
上的圆![]() 与
与![]() 轴相切,且
轴相切,且![]() 关于点
关于点![]() 对称.
对称.
(1)求![]() 和
和![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,与
,与![]() 交于
交于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com