
【题目】数列![]() 的前n项
的前n项![]()
![]() 组成集合
组成集合![]() ,从集合
,从集合![]() 中任取
中任取![]() 个数,其所有可能的k个数的乘积的和为
个数,其所有可能的k个数的乘积的和为![]() (若只取一个数,规定乘积为此数本身),例如:对于数列
(若只取一个数,规定乘积为此数本身),例如:对于数列![]() ,当
,当![]() 时,
时,![]()
![]()
![]() 时,
时,![]()
![]()
![]() ;
;
(1)若集合![]() ,求当
,求当![]() 时,
时,![]()
![]()
![]() 的值;
的值;
(2)若集合![]() ,证明:
,证明:![]() 时集合
时集合![]() 的
的![]() 与
与![]() 时集合
时集合![]() 的
的![]() (为了以示区别,用
(为了以示区别,用![]() 表示)有关系式
表示)有关系式![]() ,其中
,其中![]()
![]() ;
;
(3)对于(2)中集合![]() .定义
.定义![]() ,求
,求![]() (用n表示).
(用n表示).
【答案】(1)![]()
![]()
![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用![]() 的定义可得
的定义可得![]()
![]()
![]() 的值.
的值.
(2)![]() 时,集合
时,集合![]() 的
的![]() 中乘积由两部分构成,一部分是乘积中含
中乘积由两部分构成,一部分是乘积中含![]() ,另一部分不含
,另一部分不含![]() ,从而可得
,从而可得![]() 之间的关系.
之间的关系.
(3)可先证明![]() 所有非空子集中各元素的乘积和为
所有非空子集中各元素的乘积和为![]() ,从而可得
,从而可得![]() .
.
(1)![]() 时,
时,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
(2)![]() 时,集合
时,集合![]() 的
的![]() 中各乘积由两部分构成,
中各乘积由两部分构成,
一部分是乘积中含因数![]() ,乘积的其他因数来自集合
,乘积的其他因数来自集合![]() ,故诸乘积和为
,故诸乘积和为![]() ;
;
另一部分不含![]() ,乘积的所有因数来自集合
,乘积的所有因数来自集合![]() ,故诸乘积的和为
,故诸乘积的和为![]() .
.
故![]() .
.
(3)我们先证明一个性质:
![]() 所有非空子集中各元素的乘积和为
所有非空子集中各元素的乘积和为![]() .
.
证明:考虑![]() 的展开式,该展开式共有
的展开式,该展开式共有![]() 项,
项,
每一项均为各因式中选取![]() 或
或![]() 后的乘积(除去各项均选1).
后的乘积(除去各项均选1).
对于![]() 的任意非空子集
的任意非空子集![]() ,
,
该集合中各元素的乘积![]() 为
为![]() 的展开式中的某一项:即第
的展开式中的某一项:即第![]() 个因式选择
个因式选择![]() ,
,![]() ,其余的因式选择1,
,其余的因式选择1,
注意到非空子集的个数为![]() ,
,
故![]() 的所有非空子集中各元素的乘积均在
的所有非空子集中各元素的乘积均在![]() 的展开式中恰好出现一次,
的展开式中恰好出现一次,
所以![]() 所有非空子集中各元素的乘积和为
所有非空子集中各元素的乘积和为![]() .
.
故对于![]() ,
,
![]()
![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校决定为本校上学所需时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学所需时间(单位:分钟),将600人随机编号为001,002,…,600,抽取的50名学生上学所需时间均不超过60分钟,将上学所需时间按如下方式分成六组,第一组上学所需时间在[0,10),第二组上学所需时间在[10,20)…,第六组上学所需时间在[50,60],得到各组人数的频率分布直方图,如下图
(1)若抽取的50个样本是用系统抽样的方法得到,且第一个抽取的号码为006,则第五个抽取的号码是多少?
(2)若从50个样本中属于第四组和第六组的所有人中随机抽取2人,设他们上学所需时间分别为a、b,求满足![]() 的事件的概率;
的事件的概率;
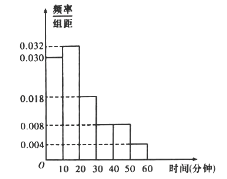
(3)设学校配备的校车每辆可搭载40名学生,请根据抽样的结果估计全校应有多少辆这样的校车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是各项均为正数的等差数列,其公差
是各项均为正数的等差数列,其公差![]() 大于零.若线段
大于零.若线段![]() ,
,![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( ).
,则( ).
A.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
B.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
C.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
D.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线l与椭圆C交于P,Q两点,且点M满足
,直线l与椭圆C交于P,Q两点,且点M满足![]() .
.
(1)若点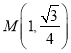 ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线l过点![]() 且不与x轴重合,过点M作垂直于l的直线
且不与x轴重合,过点M作垂直于l的直线![]() 与y轴交于点
与y轴交于点![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加诗词大赛,各答3道题,每人答对每道题的概率均为![]() ,且各人是否答对每道题互不影响.
,且各人是否答对每道题互不影响.
(Ⅰ)用![]() 表示甲同学答对题目的个数,求随机变量
表示甲同学答对题目的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“甲比乙答对题目数恰好多2”,求事件
为事件“甲比乙答对题目数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com