分析:(1)先证明四边形AOED是平行四边形,即可得到 DE∥OA,从而证得DE∥面ABC.
(2)由CA⊥AB,且AA
1⊥CA,可得CA⊥面AA
1B
1B,即CA为四棱锥的高,设圆柱高为h,底半径为r,则V
柱=πr
2h,求出椎体的体积,即可得到四棱锥C-ABB
1A
1与圆柱OO
1的体积比.
(3)先证 A
1O
1⊥面CBB
1C
1,则∠A
1CO
1为CA
1与面BB
1C所成的角,在Rt△A
1O
1C中,由
sin∠A1CO1=求得CA
1与面BB
1C所成角的正弦值.
解答: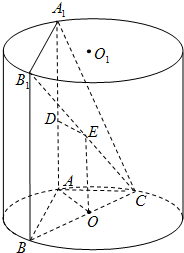
解:(1)证明:连接EO,OA.∵E,O分别为B
1C,BC的中点,∴EO∥BB
1.
又DA∥BB
1,且
DA=EO=BB1.∴四边形AOED是平行四边形,
即DE∥OA,DE?面ABC.∴DE∥面ABC.
(2)由题DE⊥面CBB
1,且由(1)知DE∥OA.∴AO⊥面CBB
1,∴AO⊥BC,
∴AC=AB.因BC是底面圆O的直径,得CA⊥AB,且AA
1⊥CA,
∴CA⊥面AA
1B
1B,即CA为四棱锥的高.
设圆柱高为h,底半径为r,则V
柱=πr
2h,
V锥=h(r)•(r)=hr2,
∴V
锥:V
柱 =
.
(3)解:作过C的母线CC
1,连接B
1C
1,则B
1C
1是上底面圆O
1的直径,
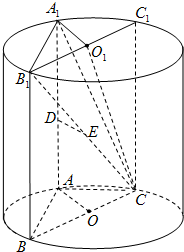
连接A
1O
1,得A
1O
1∥AO,又AO⊥面CBB
1C
1,
∴A
1O
1⊥面CBB
1C
1,连接CO
1,
则∠A
1CO
1为CA
1与面BB
1C所成的角,
设BB
1=BC=2,则
A1C==,
A
1O
1=1.(12分)
在Rt△A
1O
1C中,
sin∠A1CO1==.
点评:本题考查证明线面平行的方法,求棱锥的体积和直线与平面成的角,找出∠A1CO1为CA1与面BB1C所成的角,是解题的难点.

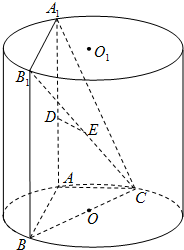 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥面CBB1.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥面CBB1. 解:(1)证明:连接EO,OA.∵E,O分别为B1C,BC的中点,∴EO∥BB1.
解:(1)证明:连接EO,OA.∵E,O分别为B1C,BC的中点,∴EO∥BB1.


 53随堂测系列答案
53随堂测系列答案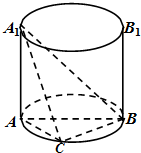 如图,AA1,BB1是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点,AA1=AB=4.
如图,AA1,BB1是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点,AA1=AB=4. 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点.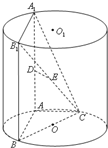 (2013•东莞一模)如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥面CBB1.
(2013•东莞一模)如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥面CBB1.