
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
【答案】(1)25,(2)0.012,(3)0.7.
【解析】![]() 试题分析:(Ⅰ)先由频率分布直方图求出[50,60)的频率,结合茎叶图中得分在[50,60)的人数即可求得本次考试的总人数;(Ⅱ)根据茎叶图的数据,利用(Ⅰ)中的总人数减去[50,80)外的人数,即可得到[50,80)内的人数,从而可计算频率分布直方图中[80,90)间矩形的高;(Ⅲ)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
试题分析:(Ⅰ)先由频率分布直方图求出[50,60)的频率,结合茎叶图中得分在[50,60)的人数即可求得本次考试的总人数;(Ⅱ)根据茎叶图的数据,利用(Ⅰ)中的总人数减去[50,80)外的人数,即可得到[50,80)内的人数,从而可计算频率分布直方图中[80,90)间矩形的高;(Ⅲ)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
(Ⅰ)分数在[50,60)的频率为0.008×10=0.08,
由茎叶图知:分数在[50,60)之间的频数为2,
∴全班人数为![]() .
.
(Ⅱ)分数在[80,90)之间的频数为25﹣22=3;
频率分布直方图中[80,90)间的矩形的高为![]() .
.
(Ⅲ)将[80,90)之间的3个分数编号为a1,a2,a3,[90,100)之间的2个分数编号为b1,b2,
在[80,100)之间的试卷中任取两份的基本事件为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)共10个,
其中,至少有一个在[90,100)之间的基本事件有7个,
故至少有一份分数在[90,100)之间的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.
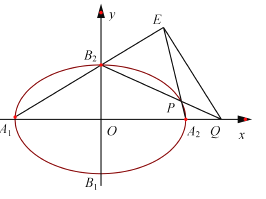
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,
,![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作直线与
作直线与![]() 交于
交于![]() 两点,求三角形
两点,求三角形![]() 面积的最大值(
面积的最大值(![]() 是坐标原点).
是坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax+(k﹣1)a﹣x(a>且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)>0,试判断函数单调性,并求使不等式f(x2+x)+f(t﹣2x)>0恒成立的t的取值范围;
(3)若f(1)= ![]() ,设g(x)=a2x+a﹣2x﹣2mf(x),g(x)在[1,+∞)上的最小值为﹣1,求m的值.
,设g(x)=a2x+a﹣2x﹣2mf(x),g(x)在[1,+∞)上的最小值为﹣1,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com