练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，曲线的参数方程为（，为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）若，求的极坐标方程；

    （2）若与恰有4个公共点，求的取值范围.

    【答案】（1）（2）

    【解析】

    （1）由参数方程消参后，可得其普通直角坐标方程，结合可求出其极坐标方程.

    （2）由题意首先确定曲线的形状为原点为圆心，半径为2和4的两个同心圆，由公共点个数判断出与圆相交，即可得关于半径的不等式，从而求出半径的取值范围.

    解：（1）由（为参数），得，

    即，得，即，

    所以的极坐标方程为.

    （2）由题意可知，则曲线表示圆心为，半径为的圆，

    由，得或，则由两个同心圆组成，原点为圆心，半径为2和4；

    因为与恰有4个公共点，所以圆与圆相交，

    所以，解得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某地计划在水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示，水库年入流量（年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上，其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年，将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.

    （1）求未来4年中，至多有1年的年入流量超过120的概率；

    （2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量限制，并有如下关系：

    年入流量

    发电机最多可运行台数

    1

    2

    3

    若某台发电机运行，则该台发电机年净利润为5000万元；若某台发电机未运行，则该台发电机年维护费与年入流量有如下关系：

    年入流量

    一台未运行发电机年维护费

    500

    800

    欲使水电站年净利润最大，应安装发电机多少台？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年3月份，上海出台了《关于建立完善本市生活垃圾全程分类体系的实施方案》，4月份又出台了《上海市生活垃圾全程分类体系建设行动计划（2018-2020年）》，提出到2020年底，基本实现单位生活垃圾强制分类全覆盖，居民区普遍推行生活垃圾分类制度．为加强社区居民的垃圾分类意识，推动社区垃圾分类正确投放，某社区在健身广场举办了“垃圾分类，从我做起”生活垃圾分类大型宣传活动，号召社区居民用实际行动为建设绿色家园贡献一份力量，为此需要征集一部分垃圾分类志愿者．

    （1）为调查社区居民喜欢担任垃圾分类志愿者是否与性别有关，现随机选取了一部分社区居民进行调查，其中被调查的男性居民和女性居民人数相同，男性居民中不喜欢担任垃圾分类志愿者占男性居民的，女性居民中不喜欢担任垃圾分类志愿者占女性居民的，若研究得到在犯错误概率不超过0.010的前提下，认为居民喜欢担任垃圾分类志愿者与性别有关，则被调查的女性居民至少多少人？

    附，，

    0.100

    0.050

    0.010

    0.005

    0.001

    2.706

    3.841

    6.635

    7.879

    10.828

    （2）某垃圾站的日垃圾分拣量（千克）与垃圾分类志愿者人数（人）满足回归直线方程，数据统计如下：

    志愿者人数（人）

    2

    3

    4

    		5

    6

    日垃圾分拣量（千克）

    25

    30

    40

    45

    已知，，，根据所给数据求和回归直线方程，附：，．

    （3）用（2）中所求的线性回归方程得到与对应的日垃圾分拣量的估计值．当分拣数据与估计值满足时，则将分拣数据称为一个“正常数据”．现从5个分拣数据中任取3个，记表示取得“正常数据”的个数，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为为参数，以坐标原点为极点，x轴的正半轴为极轴建建立极坐标系，曲线C的极坐标方程为．

    求曲线C的直角坐标方程与直线l的极坐标方程；

    Ⅱ若直线与曲线C交于点不同于原点，与直线l交于点B，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）求函数的极值；

    （Ⅱ）若实数为整数，且对任意的时，都有恒成立，求实数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，将曲线：上的点按坐标变换，得到曲线，为与轴负半轴的交点，经过点且倾斜角为的直线与曲线的另一个交点为，与曲线的交点分别为，（点在第二象限）.

    （Ⅰ）写出曲线的普通方程及直线的参数方程；

    （Ⅱ）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是一个由正四棱锥和正四棱柱构成的组合体，正四棱锥的侧棱长为6，为正四棱锥高的4倍.当该组合体的体积最大时，点到正四棱柱外接球表面的最小距离是（ ）

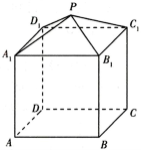
    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某工厂的一个车间抽取某种产品50件，产品尺寸（单位：cm）落在各个小组的频数分布如下表：

    数据分组

    [12.5，15.5）

    [15.5，18.5）

    [18.5，21.5）

    [21.5，24.5）

    [24.5，27.5）

    [27.5，30.5）

    [30.5，33.5）

    频数

    3

    8

    9

    12

    10

    5

    3

    （1）根据频数分布表，求该产品尺寸落在[27.5，33.5]内的概率；

    （2）求这50件产品尺寸的样本平均数（同一组中的数据用该组区间的中点值作代表）；

    （3）根据频数分布对应的直方图，可以认为这种产品尺寸服从正态分布，其中近似为样本平均值，近似为样本方差，经计算得.利用该正态分布，求（）.

    附：（1）若随机变量服从正态分布，则；（2）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某品牌布娃娃做促销活动：已知有50个布娃娃，其中一些布娃娃里面有奖品，参与者可以先在50个布娃娃中购买5个，看完5个布娃娃里面的结果再决定是否将剩下的布娃娃全部购买，设每个布娃娃有奖品的概率为，且各个布娃娃是否有奖品相互独立.

    （1）记5个布娃娃中有1个有奖品的概率为，当时，的最大值，求；

    （2）假如这5个布娃娃中恰有1个有奖品，以上问中的作为p的值.已知每次购买布娃娃需要2元，若有中奖，则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据，是否该买下剩下所有的45个布娃娃；

    （3）若已知50件布娃娃中有10个布娃娃有奖品，从这堆布娃娃中任意购买5个，若抽到k个有奖品可能性最大，求k的值.（k为正整数）

    查看答案和解析>>

    同步练习册答案