
(满分15分)定义在R上的函数f(x)=ax3+bx2+cx+d满足:函数f(x)的图象关于原点对称;函数f(x)的图象过点(3,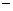 6);函数f(x)在点x1,x2处取得极值,且|x1
6);函数f(x)在点x1,x2处取得极值,且|x1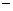 x2|=4.
x2|=4.
(1)求f(x)表达式;
(2)求函数f(x)在点P(3,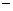 6)处切线方程;
6)处切线方程;
(3)若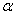 、
、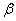 ∈R,求证:
∈R,求证: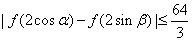 .
.
 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com