
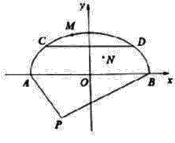
����Ŀ��ij���ÿ������滮Ҫ��һ����ͣ������ͣ�������������ͼ��ʾ����Բ��AMB������APΪ2���ף�BPΪ4���ף�![]() ��MΪ����Բ������A��B��һ���㣬��
��MΪ����Բ������A��B��һ���㣬��![]() ������ֵΪ
������ֵΪ![]() ƽ�����ף���ͼ��ϵ��
ƽ�����ף���ͼ��ϵ��
![]() �������Բ���ķ��̣�
�������Բ���ķ��̣�
![]() ��Ҫ��������ͣ�����ڳ������˵�ָ��λ��P����NΪ�����㣬��A,BΪ���ڣ�Ҫʹ������ʡ�������̲���Ҫָ��һ���ֽ��ߣ�������ֽ������ڵ����߷��̣�
��Ҫ��������ͣ�����ڳ������˵�ָ��λ��P����NΪ�����㣬��A,BΪ���ڣ�Ҫʹ������ʡ�������̲���Ҫָ��һ���ֽ��ߣ�������ֽ������ڵ����߷��̣�
![]() ���ڰ���Բ��ͣ�������Ϸ��������̳������ε�һ��CD��ABƽ�У���
���ڰ���Բ��ͣ�������Ϸ��������̳������ε�һ��CD��ABƽ�У���![]() ���ף���ȷ��t��ֵ��ʹ�̳������������
���ף���ȷ��t��ֵ��ʹ�̳������������
���𰸡�![]()
![]()
![]()
![]()
![]()
��������
��1����ֱ��������PAB�У�����֪��Ϲ��ɶ�����AB������Բ����Ϊ![]() ��a��b��0��������֪��ʽ���a��b������Բ���̿���
��a��b��0��������֪��ʽ���a��b������Բ���̿���
��2������N��P��·����ȣ��ɵ�NA+AP��NB+BP����NA��NB��2��AB����N����A��BΪ�����˫�����ϣ���˫���߷���Ϊ![]() ��m��0��n��0������
��m��0��n��0������![]() �����m��n��ֵ����˫���߷��̿���
�����m��n��ֵ����˫���߷��̿���
��3����CD��2t����D��t��s����s��0������![]() �����s�����̳������Ϊy��2ts��2t
�����s�����̳������Ϊy��2ts��2t![]() ��Ȼ�����û�������ʽ����ֵ��
��Ȼ�����û�������ʽ����ֵ��
![]() ��ֱ��������PAB�У�
��ֱ��������PAB�У�![]() ��
��![]() ��
��
�ɹ��ɶ����ã�![]() ��
��
����Բ����Ϊ![]() ��
��
�������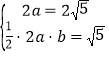 �����
�����![]() ��
��![]() ��
��
![]() ��Բ���ķ���Ϊ
��Բ���ķ���Ϊ![]() ��
��
![]() �ɵ�N��P��·����ȣ�
�ɵ�N��P��·����ȣ�![]() ����
����![]() ��
��
��![]() ��
��![]() ����A��BΪ�����˫�����ϣ�
����A��BΪ�����˫�����ϣ�
��˫���߷���Ϊ![]() ��
��
��![]() �����
�����![]() ��
��![]() ��
��
![]() ˫���߷���Ϊ
˫���߷���Ϊ![]() ��
��
![]() ��
��![]() ����
����![]() ����
����![]() ��
��
![]() ��
��
![]() �̳������Ϊy��2ts��2t
�̳������Ϊy��2ts��2t![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��
���ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ��������
��������
![]() ��
��![]() ʱ���̳������������Ϊ
ʱ���̳������������Ϊ![]() ƽ�����ף�
ƽ�����ף�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��
��1������![]() ͼ����
ͼ����![]() �������߷��̣�
�������߷��̣�
��2��֤����![]() ��
��
��3��������ʽ![]() ���������
���������![]() ����������ʵ��
����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() ����
���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() �ߵ��е㣬�ְ�
�ߵ��е㣬�ְ�![]() ��
��![]() �۵���ʹ����
�۵���ʹ����![]() ������ͼ2��ʾ������
������ͼ2��ʾ������![]() ����
����![]() .
.
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() �нǵ�����ֵ.
�нǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���л���֪ʶ�����������ֳ����;��������֣���������ѡ��ѡһ���һ��ķ�ʽ���У�ÿλѡ�������5��ѡ�����Ļ��ᣬѡ���ۻ����3�����3�⼴��ֹ������ı��������3����ֱ�ӽ�����������3��������̭.��֪ѡ�ּ״��ÿ������ĸ�����ͬ�������֮��û��Ӱ�죬�����������δ���ĸ���Ϊ![]() .
.
��1����ѡ�ּɽ�������ĸ���.
��2����ѡ�ּ��ڳ����д���ĸ���Ϊ![]() ������
������![]() �ķֲ��У�����
�ķֲ��У�����![]() ����ѧ����.
����ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���ڿ�ѧ��������һ���ľߺн����Դ�ҵ����һ����ѧ���ڣ�ÿ�۳�1�иò�Ʒ������30Ԫ��δ�۳��IJ�Ʒ��ÿ�п���10Ԫ.������ʷ���ϣ��õ���ѧ���г���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ.��ͬѧΪ�����ѧ��������160�иò�Ʒ����![]() ����λ:�У�
����λ:�У� ![]() ����ʾ�����ѧ���ڵ��г���������
����ʾ�����ѧ���ڵ��г��������� ![]() ����λ:Ԫ����ʾ�����ѧ���ھ����ò�Ʒ������.
����λ:Ԫ����ʾ�����ѧ���ھ����ò�Ʒ������.
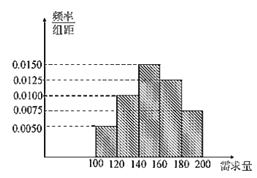
��1������ֱ��ͼ���������ѧ�����г�������![]() ��ƽ������
��ƽ������
��2����![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
��3������ֱ��ͼ��������![]() ������4000Ԫ�ĸ���.
������4000Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ������ϵ�ĵ�һ�����ڵ���������![]() ��
��![]() �����¶���:
�����¶���:![]() ,��ô�Ƶ�
,��ô�Ƶ�![]() �ǵ�
�ǵ�![]() �ġ���λ�㡱��ͬʱ��
�ġ���λ�㡱��ͬʱ��![]() �ǵ�
�ǵ�![]() �ġ���λ�㡱.
�ġ���λ�㡱.
��1����д����![]() ��һ������λ�㡱�����һ������λ�㡱���ꣻ
��һ������λ�㡱�����һ������λ�㡱���ꣻ
��2����![]() ��
��![]() ��
��![]() ��
��![]() ��Ϊ�������ҵ�
��Ϊ�������ҵ�![]() �ǵ�
�ǵ�![]() ����λ�㣬���жϵ�
����λ�㣬���жϵ�![]() �Ƿ���ǵ�
�Ƿ���ǵ�![]() �ġ���λ�㡱���ǵ�
�ġ���λ�㡱���ǵ�![]() �ġ���λ�㡱���������֤�������������˵�����ɣ�
�ġ���λ�㡱���������֤�������������˵�����ɣ�
��3����������![]() ��������������������ʵ��
��������������������ʵ��![]() ���ܴ���
���ܴ���![]() ��ʹ�õ�
��ʹ�õ�![]() ���ǵ�
���ǵ�![]() �ġ���λ�㡱�����ǵ�
�ġ���λ�㡱�����ǵ�![]() �ġ���λ�㡱����������
�ġ���λ�㡱����������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2018���Ĵ�ʡ�ɶ��е�����ѧ������ѧ��ģ�⡿��֪��Բ![]() ��һ������
��һ������![]() ���ҹ���
���ҹ���![]() ���Ҷ���Ϊ
���Ҷ���Ϊ![]() ��������
��������![]() �Ķ�ֱ��
�Ķ�ֱ��![]() ����Բ����
����Բ����![]() ����.
����.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2��![]() ����Բ
����Բ![]() ��һ�㣬
��һ�㣬 ![]() �Ľ�ƽ���߽�
�Ľ�ƽ���߽�![]() ����
����![]() ����
����![]() �ij���
�ij���
��3����![]() �����Ƿ����һ��
�����Ƿ����һ��![]() ��ʹ�õ�
��ʹ�õ�![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ����
����![]() �ϣ������ڣ����
�ϣ������ڣ����![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
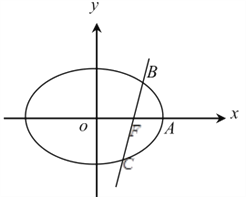
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC������ԭ�㣬������x���ϣ����ҽ���ֱ�ΪF1��F2����|F1F2|=2���㣨1��![]() ������ԲC�ϣ�
������ԲC�ϣ�
��1������ԲC�ķ��̣�
��2����F1��ֱ��l����ԲC�ཻ��A��B���㣬����AF2B�����Ϊ![]() ������F2ΪԲ������ֱ��l���е�Բ�ķ��̣�
������F2ΪԲ������ֱ��l���е�Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��1(a>b>0)�ϵĵ�P������������F1��F2�ľ���֮��Ϊ2
��1(a>b>0)�ϵĵ�P������������F1��F2�ľ���֮��Ϊ2![]() ��������Ϊ
��������Ϊ![]() .
.
(1)����Բ�ı����̣�
(2)���ҽ���F2��ֱ��l����Բ��A��B���㣬��y����һ��M(0��![]() )����|MA|��|MB|����ֱ��l��б��k��ֵ��
)����|MA|��|MB|����ֱ��l��б��k��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com