
【题目】设不等式组 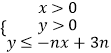 所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记 ![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
【答案】
(1)解:画出 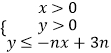 的可行域
的可行域

f(1)=2+1=3
f(2)=3+2+1=6
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n
(2)解:由题意知:bn=3n2n
Sn=321+622+923+…+3(n﹣1)2n﹣1+3n2n
∴2Sn=322+623+…+3(n﹣1)2n+3n2n+1
∴﹣Sn=321+322+323+…32n﹣3n2n+1
=3(2+22+…+2n)﹣3n2n+1
=3 ![]()
=3(2n+1﹣2)﹣3nn+1
∴﹣Sn=(3﹣3n)2n+1﹣6
Sn=6+(3n﹣3)2n+1
(3)解: ![]()

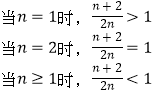
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3= ![]()
∴m≥ ![]() .
.
【解析】(1)据可行域,求出当x=1,x=2时,可行域中的整数点,分别求出f(1),f(2),f(n).(2)由于数列的通项是一个等差数列与一个等比数列的积构成的新数列,利用错位相减的方法求出数列的和.(3)求出 ![]() ,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
【考点精析】解答此题的关键在于理解二元一次不等式(组)所表示的平面区域的相关知识,掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
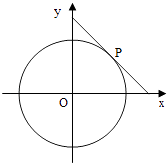
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1: ![]() ﹣
﹣ ![]() =1过点P且离心率为
=1过点P且离心率为 ![]() .
. 
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 写出曲线
写出曲线![]() 的极坐标的方程以及曲线
的极坐标的方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若过点
若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.
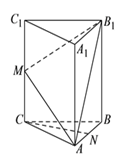
(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长
的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com