
【题目】某市一个社区微信群“步行者”有成员100人,其中男性70人,女性30人,现统计他们平均每天步行的时间,得到频率分布直方图,如图所示:

若规定平均每天步行时间不少于2小时的成员为“步行健将”,低于2小时的成员为“非步行健将”.已知“步行健将”中女性占![]() .
.
(1)填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;

(2)现从“步行健将”中随机选派2人参加全市业余步行比赛,求2人中男性的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]() .
.

科目:高中数学 来源: 题型:
【题目】养正中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),校总务处计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设![]() (单位:弧度),用
(单位:弧度),用![]() 表示弓形BCD的面积
表示弓形BCD的面积![]()
(2)如果该校总务处邀请你规划这块土地。如何设计![]() 的大小才能使总利润最大?并求出该最大值
的大小才能使总利润最大?并求出该最大值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在 △ABC 中,设 a,b,c 分别是角 A,B,C 的对边,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(Ⅰ)若点O到直线l的距离为![]() , 求直线l的方程;
, 求直线l的方程;
(Ⅱ)设点A是直线l与抛物线C在第一象限的交点.点B是以点F为圆心,|FA|为半径的圆与x轴负半轴的交点.试判断直线AB与抛物线C的位置关系,并给出证明.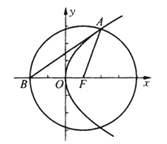
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a2=2,a4=![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的![]() 班和文史类专业的
班和文史类专业的![]() 班各抽取
班各抽取![]() 名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
优秀 | 非优秀 | 总计 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
附:参考公式及数据:
(1)统计量:![]() ,(
,(![]() ).
).
(2)独立性检验的临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
则下列说法正确的是
A. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
B. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关
C. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
D. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD的三个顶点的坐标为![]()
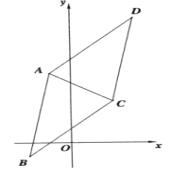
(1)求平行四边形ABCD的顶点D的坐标;
(2)求四边形ABCD的面积
(3)求![]() 的平分线所在直线方程。
的平分线所在直线方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
A.![]() >
> ![]()
![]()
B.ln(x2+1)>ln(y2+1)
C.sinx>siny
D.x3>y3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com