
分析 通过对an+1+an=2n-3变形、整理可知数列{an-n+2}是首项为3、公比为-1的等比数列,进而计算可得结论.
解答 解:∵an+1+an=2n-3,
∴an+1=-an+2n-3
=-an+(n+1)+n-4
=-an+(n+1)+n-2-2,
整理得:an+1-(n+1)+2=-an+n-2=-(an-n+2),
又∵a1-1+2=2-1+2=3,
∴数列{an-n+2}是首项为3、公比为-1的等比数列,
∴an-n+2=3×(-1)n-1,an=n-2+3×(-1)n-1,
∴a8-a4=(8-2-3)-(4-2-3)=4,
故答案为:4.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p=-1,q=6 | B. | p=1,q=6 | C. | p=-1,q=-6 | D. | p=1,q=-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(x,y,z)中x,y,z的位置可以互换的 | |
| B. | 空间直角坐标系中的点与一个三元有序数组是一种一一对应关系 | |
| C. | 空间直角坐标系中的三条坐标轴把空间分成八个部分 | |
| D. | 某点在不同空间直角坐标系中的坐标位置可以相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
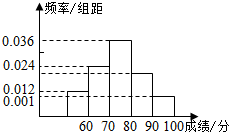 对某班的全体学生一次数学测试成绩进行分析,数据的分组情况为:[50,60)[60,70)[70,80)[80,90)[90,100),频率分布直方图如图:
对某班的全体学生一次数学测试成绩进行分析,数据的分组情况为:[50,60)[60,70)[70,80)[80,90)[90,100),频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(cosA)>f(cosB) | B. | f(sinA)>f(sinB) | C. | f(sinA)>f(cosB) | D. | f(sinA)<f(cosB) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com