
 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥面CDE;③MN∥CE;④MN、CE异面其中正确结论的序号是________.
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥面CDE;③MN∥CE;④MN、CE异面其中正确结论的序号是________.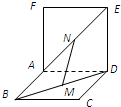 ∵两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,
∵两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,

科目:高中数学 来源: 题型:
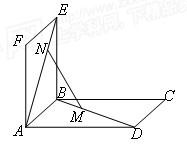 如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM.
如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM.查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第77课时):第九章 直线、平面、简单几何体-空间向量的坐标运算(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com