
ЁОЬтФПЁПФГЪаЛ§МЋГЋЕМбЇЩњВЮгыТЬЩЋЛЗБЃЛюЖЏЃЌЦфжаДњКХЮЊЁАЛЗБЃЮРЪПЁЊ12369ЁБЕФТЬЩЋЛЗБЃЛюЖЏаЁзщЖд2014Фъ1дТЁЊ2014Фъ12дТЃЈвЛФъЃЉФкПеЦјжЪСПжИЪ§![]() НјааМрВтЃЌЯТБэЪЧдкетвЛФъЫцЛњГщШЁЕФ100ЬьЕФЭГМЦНсЙћЃК
НјааМрВтЃЌЯТБэЪЧдкетвЛФъЫцЛњГщШЁЕФ100ЬьЕФЭГМЦНсЙћЃК
жИЪ§API | [0ЃЌ50] | ЃЈ50ЃЌ100] | ЃЈ100ЃЌ150] | ЃЈ150ЃЌ200] | ЃЈ200ЃЌ250] | ЃЈ250ЃЌ300] | >300 |
ПеЦјжЪСП | гХ | СМ | ЧсЮЂЮлШО | ЧсЖШЮлШО | жаЖШЮлШО | жажиЖШЮлШО | жиЖШЮлШО |
ЬьЪ§ | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
ЃЈ1ЃЉШєФГЪаФГЦѓвЕУПЬьгЩПеЦјЮлШОдьГЩЕФОМУЫ№ЪЇ![]() ЃЈЕЅЮЛЃКдЊЃЉгыПеЦјжЪСПжИЪ§
ЃЈЕЅЮЛЃКдЊЃЉгыПеЦјжЪСПжИЪ§![]() ЃЈМЧЮЊ
ЃЈМЧЮЊ![]() ЃЉЕФЙиЯЕЮЊЃК
ЃЉЕФЙиЯЕЮЊЃК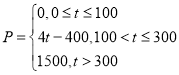 ЃЌдкетвЛФъФкЫцЛњГщШЁвЛЬьЃЌЙРМЦИУЬьОМУЫ№ЪЇ
ЃЌдкетвЛФъФкЫцЛњГщШЁвЛЬьЃЌЙРМЦИУЬьОМУЫ№ЪЇ![]() дЊЕФИХТЪЃЛ
дЊЕФИХТЪЃЛ
ЃЈ2ЃЉШєБОДЮГщШЁЕФбљБОЪ§Онга30ЬьЪЧдкЙЉХЏМОНкЃЌЦфжага8ЬьЮЊжиЖШЮлШОЃЌ![]() СаСЊБэЃЌВЂХаЖЯЪЧЗёга
СаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊФГЪаБОФъЖШПеЦјжиЖШЮлШОгыЙЉХЏгаЙиЃП
ЕФАбЮеШЯЮЊФГЪаБОФъЖШПеЦјжиЖШЮлШОгыЙЉХЏгаЙиЃП
ЗЧжиЖШЮлШО | жиЖШЮлШО | КЯМЦ | |
ЙЉХЏМО | |||
ЗЧЙЉХЏМОНк | |||
КЯМЦ | 100 |
ЯТУцСйНчжЕБэЙЉВЮПМЃЎ
| 0ЃЎ15 | 0ЃЎ10 | 0ЃЎ05 | 0ЃЎ025 | 0ЃЎ010 | 0ЃЎ005 | 0ЃЎ001 |
| 2ЃЎ072 | 3ЃЎ841 | 5ЃЎ024 | 6ЃЎ635 | 7ЃЎ879 | 10ЃЎ828 |
ВЮПМЙЋЪНЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉга95%ЕФАбЮеШЯЮЊФГЪаБОФъЖШПеЦјжиЖШЮлШОгыЙЉХЏгаЙиЃЎ
ЃЛЃЈ2ЃЉга95%ЕФАбЮеШЯЮЊФГЪаБОФъЖШПеЦјжиЖШЮлШОгыЙЉХЏгаЙиЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЬтвтжЊжЛПЩФмЪЧЕкЖўЖЮКЏЪ§дкДЫЗЖЮЇРрЃЌДгЖјЕУЕН![]() ЕФЗЖЮЇЃЌНјЖјЭЈЙ§ЦЕЪ§ЭГМЦБэЕУЕНЫљЖдгІЕФЬьЪ§ЃЌРћгУЙХЕфИХаЭИХТЪЙЋЪНЕУЦфИХТЪЃЛЃЈ2ЃЉСаСЊБэЕФЭъГЩжЛвЊевЕНИїИіЪ§ОнЫљЖдгІЕФКЌвхВЛФбЭъГЩЃЌШЛКѓРћгУЖРСЂадМьбщЯрЙиЯЕЪ§ПДЯрЙиадДѓаЁЃЎ
ЕФЗЖЮЇЃЌНјЖјЭЈЙ§ЦЕЪ§ЭГМЦБэЕУЕНЫљЖдгІЕФЬьЪ§ЃЌРћгУЙХЕфИХаЭИХТЪЙЋЪНЕУЦфИХТЪЃЛЃЈ2ЃЉСаСЊБэЕФЭъГЩжЛвЊевЕНИїИіЪ§ОнЫљЖдгІЕФКЌвхВЛФбЭъГЩЃЌШЛКѓРћгУЖРСЂадМьбщЯрЙиЯЕЪ§ПДЯрЙиадДѓаЁЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЁАдкБОФъФкЫцЛњГщШЁвЛЬьЃЌИУЬьОМУЫ№ЪЇ![]() дЊЁБЮЊЪТМў
дЊЁБЮЊЪТМў![]() ЃЌ
ЃЌ
гЩ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЦЕЪ§ЮЊ39ЃЌ
ЃЌЦЕЪ§ЮЊ39ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЃЈ2ЃЉИљОнвдЩЯЪ§ОнЕУЕНШчБэЃК
ЗЧжиЖШЮлШО | жиЖШЮлШО | КЯМЦ | |
ЙЉХЏМО | 22 | 8 | 30 |
ЗЧЙЉХЏМО | 63 | 7 | 70 |
КЯМЦ | 85 | 15 | 100 |
![]() ЕФЙлВтжЕ
ЕФЙлВтжЕ![]() ЃЌ
ЃЌ
Ыљвдга95%ЕФАбЮеШЯЮЊФГЪаБОФъЖШПеЦјжиЖШЮлШОгыЙЉХЏгаЙиЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЃЌ
ЃЌ ![]() БпЩЯЕФжаЯп
БпЩЯЕФжаЯп![]() ЫљдкжБЯпЗНГЬЮЊ
ЫљдкжБЯпЗНГЬЮЊ![]() ЃЌ
ЃЌ ![]() БпЩЯЕФИп
БпЩЯЕФИп![]() ЫљдкжБЯпЗНГЬЮЊ
ЫљдкжБЯпЗНГЬЮЊ![]() ЃЎЁЁ
ЃЎЁЁ
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓжБЯп![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭцОпЩњВњЙЋЫОУПЬьМЦЛЎЩњВњЮРБјЁЂЦяБјЁЂЩЁБјетШ§жжЭцОпЙВ![]() ИіЃЌЩњВњвЛИіЮРБјаш
ИіЃЌЩњВњвЛИіЮРБјаш![]() ЗжжгЃЌЩњВњвЛИіЦяБјаш
ЗжжгЃЌЩњВњвЛИіЦяБјаш![]() ЗжжгЃЌЩњВњвЛИіЩЁБјаш
ЗжжгЃЌЩњВњвЛИіЩЁБјаш![]() ЗжжгЃЌвбжЊзмЩњВњЪБМфВЛГЌЙ§
ЗжжгЃЌвбжЊзмЩњВњЪБМфВЛГЌЙ§![]() аЁЪБЃЌШєЩњВњвЛИіЮРБјПЩЛёРћШѓ
аЁЪБЃЌШєЩњВњвЛИіЮРБјПЩЛёРћШѓ![]() дЊЃЌЩњВњвЛИіЦяБјПЩЛёРћШѓ
дЊЃЌЩњВњвЛИіЦяБјПЩЛёРћШѓ![]() дЊЃЌЩњВњвЛИіЩЁБјПЩЛёРћШѓ
дЊЃЌЩњВњвЛИіЩЁБјПЩЛёРћШѓ![]() дЊ.
дЊ.
ЃЈ1ЃЉгУУПЬьЩњВњЕФЮРБјИіЪ§![]() гыЦяБјИіЪ§
гыЦяБјИіЪ§![]() БэЪОУПЬьЕФРћШѓ
БэЪОУПЬьЕФРћШѓ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЃЈ2ЃЉдѕУДЗжХфЩњВњШЮЮёВХФмЪЙУПЬьЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
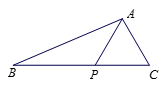
ЁОЬтФПЁПШчЭМ, дкЁї![]() жа, Еу
жа, Еу![]() дк
дк![]() БпЩЯ,
БпЩЯ, ![]() .
.
ЃЈЂёЃЉЧѓ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉШєЁї![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() , Чѓ
, Чѓ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
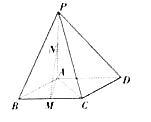
ЁОЬтФПЁПШчЭМЃКдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ ![]() ЃЌ
ЃЌ ![]() ЦНУц
ЦНУц![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЧв
ЕФжаЕуЃЌЧв![]() .
.
ЃЈ1ЃЉжЄУїЃК ![]() Уц
Уц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЛ
ЕФЬхЛ§ЃЛ
ЃЈ3ЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЦНУц
ЦНУц![]() ЃЛШєДцдкЃЌЧѓГі
ЃЛШєДцдкЃЌЧѓГі![]() ЕФГЄЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФГЄЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШЋМЏU=RЃЌМЏКЯA={x|4Ём2xЃМ128}ЃЌB={x|1ЃМxЁм6}ЃЌM={x|aЉ3ЃМxЃМa+3}ЃЎ
ЃЈ1ЃЉЧѓAЁЩUBЃЛ
ЃЈ2ЃЉШєMЁШUB=RЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаСНЫљИпжаЗжБ№зщжЏВПЗжбЇЩњВЮМгСЫЁАЦпЮхЦеЗЈЭјТчжЊЪЖДѓШќЁБЃЌЯжДгетСНЫљбЇаЃЕФВЮШќбЇЩњжаЗжБ№ЫцЛњГщШЁ30УћбЇЩњЕФГЩМЈЃЈАйЗжжЦЃЉзїЮЊбљБОЃЌЕУЕНбљБОЪ§ОнЕФОЅвЖЭМШчЭМЫљЪОЃЎ
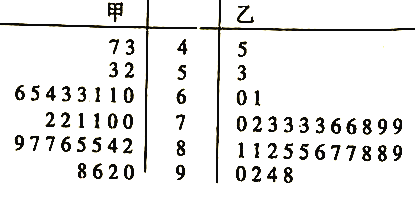
ЃЈЂёЃЉШєвваЃУПЮЛбЇЩњБЛГщШЁЕФИХТЪЮЊ0.15ЃЌЧѓвваЃВЮШќбЇЩњзмШЫЪ§ЃЛ
ЃЈЂђЃЉИљОнОЅвЖЭМЃЌДгЦНОљЫЎЦНгыВЈЖЏЧщПіСНИіЗНУцЗжЮіМзЁЂввСНаЃВЮШќбЇЩњГЩМЈЃЈВЛвЊЧѓМЦЫуЃЉЃЛ
ЃЈЂѓЃЉДгбљБОГЩМЈЕЭгк60ЗжЕФбЇЩњжаЫцЛњГщШЁ3ШЫЃЌЧѓ3ШЫВЛдкЭЌвЛбЇаЃЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбаОПЫљМЦЛЎРћгУЁАЩёЦпЁБгюжцЗЩДЌНјаааТВњЦЗДюдиЪЕбщЃЌМЦЛЎДюдиаТВњЦЗ![]() ЁЂ
ЁЂ![]() ЃЌИУЫљвЊИљОнИУВњЦЗЕФбажЦГЩБОЁЂВњЦЗжиСПЁЂДюдиЪЕбщЗбгУЁЂКЭдЄМЦВњЩњЪевцРДОіЖЈОпЬхАВХХЃЎЭЈЙ§ЕїВщЃЌгаЙиЪ§ОнШчЯТБэЃК
ЃЌИУЫљвЊИљОнИУВњЦЗЕФбажЦГЩБОЁЂВњЦЗжиСПЁЂДюдиЪЕбщЗбгУЁЂКЭдЄМЦВњЩњЪевцРДОіЖЈОпЬхАВХХЃЎЭЈЙ§ЕїВщЃЌгаЙиЪ§ОнШчЯТБэЃК
ВњЦЗA(Мў) | ВњЦЗB(Мў) | ||
бажЦГЩБОЁЂДюдиЗбгУжЎКЭ(ЭђдЊ) | 20 | 30 | МЦЛЎзюДѓзЪН№Жю300ЭђдЊ |
ВњЦЗжиСПЃЈЧЇПЫЃЉ | 10 | 5 | зюДѓДюдижиСП110ЧЇПЫ |
дЄМЦЪевцЃЈЭђдЊЃЉ | 80 | 60 |
ШчКЮАВХХетСНжжВњЦЗЕФМўЪ§НјааДюди,ВХФмЪЙзмдЄМЦЪевцДяЕНзюДѓ,зюДѓЪевцЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxoyжаЃЌвбжЊжааФдкдЕуЃЌНЙЕудкxжсЩЯЕФЫЋЧњЯпCЕФРыаФТЪЮЊ![]() ЃЌЧвЫЋЧњЯпCгыаБТЪЮЊ2ЕФжБЯпlЯрНЛЃЌЧвЦфжавЛИіНЛЕуЮЊPЃЈЉ3ЃЌ0ЃЉЃЎ
ЃЌЧвЫЋЧњЯпCгыаБТЪЮЊ2ЕФжБЯпlЯрНЛЃЌЧвЦфжавЛИіНЛЕуЮЊPЃЈЉ3ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓЫЋЧњЯпCЕФЗНГЬМАЫќЕФНЅНќЯпЗНГЬЃЛ
ЃЈ2ЃЉЧѓвджБЯпlгызјБъжсЕФНЛЕуЮЊНЙЕуЕФХзЮяЯпЕФБъзМЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com