
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为常数,函数
为常数,函数![]() 和
和![]() 的图象在它们与坐标轴交点处的切线互相平行.
的图象在它们与坐标轴交点处的切线互相平行.
(1)求![]() 的值;
的值;
(2)若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)分别求出![]() 与
与![]() 与y轴和x轴的交点坐标,求出两函数在与坐标轴交点处的导数,由导数值相等求得a的值;
与y轴和x轴的交点坐标,求出两函数在与坐标轴交点处的导数,由导数值相等求得a的值;
(2)由(1)中求得的a值得到![]() 的解析式,代入
的解析式,代入![]() ,把存在
,把存在![]() 使不等式恒成立转化为存在
使不等式恒成立转化为存在![]() ,不等式
,不等式![]() 恒成立,构造函数
恒成立,构造函数![]() ,
,![]() ,利用导数求其最大值后得答案;
,利用导数求其最大值后得答案;
(3)把![]() ,
,![]() 代入
代入![]() ,去绝对值后得到
,去绝对值后得到![]() (
(![]() ),借助于两个辅助函数
),借助于两个辅助函数![]() (
(![]() ),
),![]() (
(![]() ),证得
),证得![]() ,
,![]() ,两式联立后得答案.
,两式联立后得答案.
(1)![]() 的图象与
的图象与![]() 轴的交点为
轴的交点为![]() ,
,![]() 的图象与
的图象与![]() 轴的交点为
轴的交点为![]() ,
,
![]() ,
,![]() (
(![]() ),由
),由![]() ,
,![]() ,得
,得![]() ;
;
(2)因为![]() ,令
,令![]() ,
,![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
因为“存在![]() ,使不等式
,使不等式![]() 成立”的充要条件是
成立”的充要条件是![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() ;
;
(3)![]() (
(![]() ),
),
记![]() (
(![]() ),因为
),因为![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
又因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,①
,①
记![]() (
(![]() ),因为
),因为![]() ,所以
,所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,②
,②
由①②可得![]() ,所以
,所以![]() ,即
,即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面组成的多面体.如将正四面体所有棱各三等分,沿三等分点从原几何体割去四个小正四面体如图所示,余下的多面体就成为一个半正多面体,若这个半正多面体的棱长为2,则这个半正多面体的体积为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在悠久灿烂的中国古代文化中,数学文化是其中的一朵绚丽的奇葩.《张丘建算经》是我国古代有标志性的内容丰富的众多数学名著之一,大约创作于公元五世纪.书中有如下问题:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈,问日益几何?”.其大意为:“有一女子擅长织布,织布的速度一天比一天快,从第二天起,每天比前一天多织相同数量的布,第一天织![]() 尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知
尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知![]() 匹
匹![]() 丈,
丈,![]() 丈
丈![]() 尺,若这一个月有
尺,若这一个月有![]() 天,记该女子这一个月中的第
天,记该女子这一个月中的第![]() 天所织布的尺数为
天所织布的尺数为![]() ,
,![]() ,对于数列
,对于数列![]() 、
、![]() ,下列选项中正确的为( )
,下列选项中正确的为( )
A.![]() B.
B.![]() 是等比数列C.
是等比数列C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为
.斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() .若
.若![]() ,
,![]() 和点
和点![]() 共线,求
共线,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节是我国民间为纪念爱国诗人屈原的一个传统节日.某市为了解端午节期间粽子的销售情况,随机问卷调查了该市1000名消费者在去年端午节期间的粽子购买量(单位:克),所得数据如下表所示:
购买量 |
|
|
|
|
|
人数 | 100 | 300 | 400 | 150 | 50 |
将烦率视为概率
(1)试求消费者粽子购买量不低于300克的概率;
(2)若该市有100万名消费者,请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求(以各区间中点值作为该区间的购买量).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次数学考试中,从甲,乙两个班级各抽取10名同学的成绩进行统计分析,他们成绩的茎叶图如图所示,成绩不小于90分为及格.

(1)从两班10名同学中各抽取一人,在有人及格的情况下,求乙班同学不及格的概率;
(2)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图对称轴为坐标轴,焦点均在![]() 轴上的两椭圆
轴上的两椭圆![]() ,
,![]() 的离心率相同且均为
的离心率相同且均为![]() ,椭圆
,椭圆![]() 过点
过点![]() 且其上顶点恰为椭圆
且其上顶点恰为椭圆![]() 的上焦点.
的上焦点.![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
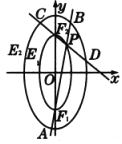
(1)求椭圆![]() ,
,![]() 的标准方程.
的标准方程.
(2)证明:![]() .
.
(3)![]() 是否为定值?若为定值.则求出该定值;否则,说明理由.
是否为定值?若为定值.则求出该定值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在区间
定义在区间![]() 上,
上,![]() ,且当
,且当![]() 时,恒有
时,恒有![]() ,又数列
,又数列![]() 满足
满足![]() ,
,![]() ,设
,设![]() ,对于任意的
,对于任意的![]() ,
,![]() 的最小自然数
的最小自然数![]() 的值为_______________________________.
的值为_______________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com