
分析 焦点在y轴上的椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{a+9}$=1的离心率为$\frac{1}{2}$,可得$\frac{\sqrt{a+9-9}}{\sqrt{a+9}}$=$\frac{1}{2}$,解得a.由b2-2bi=14+5b+b2i,利用复数相等可得$\left\{\begin{array}{l}{{b}^{2}=14+5b}\\{-2b={b}^{2}}\end{array}\right.$,解得b.由数列{cn}的首项为$\frac{a}{3}$,公比为-b,可得cn=2n-1.且存在两项cm,cn,使得$\sqrt{{c}_{m}{c}_{n}}$=2c1,利用通项公式可得:m+n=4.利用“乘1法”可得$\frac{1}{m}$+$\frac{9}{n}$=$\frac{1}{4}$(m+n)$(\frac{1}{m}+\frac{9}{n})$=$\frac{1}{4}$$(10+\frac{n}{m}+\frac{9m}{n})$,再利用基本不等式的性质即可得出.
解答 解:∵焦点在y轴上的椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{a+9}$=1的离心率为$\frac{1}{2}$,∴$\frac{\sqrt{a+9-9}}{\sqrt{a+9}}$=$\frac{1}{2}$,解得a=3.
由b2-2bi=14+5b+b2i,可得$\left\{\begin{array}{l}{{b}^{2}=14+5b}\\{-2b={b}^{2}}\end{array}\right.$,解得b=-2.
∵数列{cn}的首项为$\frac{a}{3}$,公比为-b,∴cn=$\frac{3}{3}$×2n-1=2n-1.
且存在两项cm,cn,使得$\sqrt{{c}_{m}{c}_{n}}$=2c1,∴$\sqrt{{2}^{m-1}•{2}^{n-1}}$=2,化为2m+n-2=22,可得m+n=4.
∴$\frac{1}{m}$+$\frac{9}{n}$=$\frac{1}{4}$(m+n)$(\frac{1}{m}+\frac{9}{n})$=$\frac{1}{4}$$(10+\frac{n}{m}+\frac{9m}{n})$$≥\frac{1}{4}$$(10+2\sqrt{\frac{n}{m}×\frac{9m}{n}})$=4,当且仅当n=3m=3时取等号.
∴$\frac{1}{m}$+$\frac{9}{n}$最小值为4.
故答案为:4.
点评 本题考查了综合考查了椭圆的标准方程及其性质、复数相等、等比数列的通项公式、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
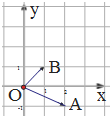 如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )
如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1-3i | D. | 1+3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-3<a<\frac{13}{4}$ | B. | $-\frac{13}{4}<a<\frac{13}{4}$ | C. | -3<a<3 | D. | $-\frac{13}{4}<a<3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com