
【题目】随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有![]() 三个旅游景点,在岸边
三个旅游景点,在岸边![]() 两地的中点处设有一个垃圾回收站点
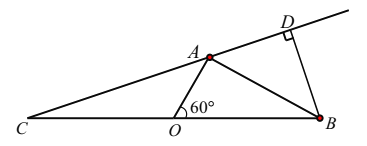
两地的中点处设有一个垃圾回收站点![]() (如图),
(如图),![]() 两地相距10
两地相距10![]() ,从回收站
,从回收站![]() 观望
观望![]() 地和
地和![]() 地所成的视角为
地所成的视角为![]() ,且
,且![]() ,设
,设![]() ;
;
(1)用![]() 分别表示
分别表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)某一时刻太阳与![]() 三点在同一直线,此时
三点在同一直线,此时![]() 地到直线
地到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]() 的最大值为10.
的最大值为10.
【解析】试题分析:(1)本题考查解三角形的实际应用,由图根据余弦定理,在![]() 中,
中, ![]() ,又因为
,又因为![]() ,所以前面的表达式转化为
,所以前面的表达式转化为![]() ,同理,在
,同理,在![]() 中,
中, ![]() ,这样结合前面得到的等式,可以用
,这样结合前面得到的等式,可以用![]() 分别表示出
分别表示出![]() 和
和![]() ;(2)由于
;(2)由于![]() ,所以
,所以![]() 的面积与
的面积与![]() 的面积相等,因此
的面积相等,因此![]() 的面积等于
的面积等于![]() ,又
,又![]() ,于是可以将
,于是可以将![]() 转化为关于
转化为关于![]() 的函数,即
的函数,即![]() ,从而转化为求函数最大值.
,从而转化为求函数最大值.
试题解析:(1)在![]() 中,
中, ![]() ,
, ![]() ,
,
由余弦定理得, ![]() ,
,
又![]() ,所以
,所以![]() ①
①
在![]() 中,
中, ![]() ,
, ![]()
由余弦定理得,
![]() ②
②
①+②得![]() ,
,
①-②得![]() ,
, ![]() ,
,
所以![]() ,即
,即![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() .
.
(2)![]() ,
,
故![]() ,
,
又![]() ,设
,设![]() ,
,
所以![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,
, ![]() 在
在![]() 上都是增函数;
上都是增函数;
所以, ![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() 的最大值为
的最大值为![]() ,即
,即![]() 的最大值为10.
的最大值为10.
(利用单调性定义证明![]() 在
在![]() 上是增函数,同样给满分;如果直接说出
上是增函数,同样给满分;如果直接说出![]() 在
在![]() 上是增函数,但未给出证明或讨论,扣1分)
上是增函数,但未给出证明或讨论,扣1分)


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如图.

(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为![]() 1,
1,![]() 2,估计
2,估计![]() 1-
1-![]() 2的值.
2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
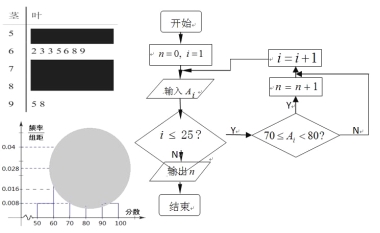
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船都要停靠在同一个泊位,它们可能在一昼夜的任意时刻到达.甲、乙两船停靠泊位的时间分别为4小时与2小时,求有一艘船停靠泊位时必需等待一段时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于
的距离之比等于![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为
所截得的线段的长为![]() ,求直线
,求直线![]() 的方程
的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各种情况下,向量终点构成什么图形?
(1)把所有单位向量的起点平移到同一点![]() ;
;
(2)把平行于某一直线的所有单位向量的起点平移到同一点;
(3)把平行于某一直线的一切向量平移到同一起点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有200名职工,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com