
【题目】某高中学校决定开展“数学知识竞赛”活动。各班级都进行了选拔,高三一班全体同学都参加了考试,将他们的分数进行统计,并作出如右图的频率分布直方图和分数的茎叶图(其中,茎叶图中仅列出了得分在![]() 的数据)
的数据)


(1)求高三一班学生的总数和频率分布直方图中a、b的值;
(2)在高三一班学生中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加学校“数学知识竞赛”,求所抽取的2名学生中至少有一人得分在[90,100]内的概率。
【答案】(1) ![]() , a=0.006,b=0.028;(2)
, a=0.006,b=0.028;(2) ![]()
【解析】
(1)由频率分布直方图求出得分在[50,60)的频率为0.16,由茎叶图得[50,60)的频数为8,由此能求出样本容量,由茎叶图得[90,100)的频数为3,由此利用频率分布直方图能求出频率分布直方图中a、b的值.
(2)竞赛成绩在80分以上(含80分)的学生有8人,其中得分在[80,90)内的学生有5人,得分在[90,100)内的学生有3人,由此能求出所抽取的2名学生中至少有一人得分在[90,100]的概率.
(1)由频率分布直方图得得分在[50,60)的频率为0.016×10=0.16,
由茎叶图得[50,60)的频数为8,
∴样本容量![]() .
.
由茎叶图得[90,100)的频数为3,
解得a=0.006,b=0.028.
(2)竞赛成绩在80分以上(含80分)的学生有50(0.010×10+0.006×10)=8人,
其中得分在[80,90)内的学生有5人,得分在[90,100)内的学生有3人,
从竞赛成绩在80分以上(含80分)的学生在随机抽取2名学生参加“全市高中数学竞赛”,
基本事件总数![]() ,
,
所抽取的2名学生中至少有一人得分在[90,100]的对立事件是抽取的两人得分都在[80,90)内,∴所抽取的2名学生中至少有一人得分在[90,100]的概率:![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某旅游胜地欲开发一座景观山,从山的侧面进行勘测,迎面山坡线![]() 由同一平面的两段抛物线组成,其中
由同一平面的两段抛物线组成,其中![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向下,
为顶点、开口向下,![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向上,以过山脚(点
为顶点、开口向上,以过山脚(点![]() )的水平线为
)的水平线为![]() 轴,过山顶(点
轴,过山顶(点![]() )的铅垂线为
)的铅垂线为![]() 轴建立平面直角坐标系如图(单位:百米).已知
轴建立平面直角坐标系如图(单位:百米).已知![]() 所在抛物线的解析式
所在抛物线的解析式![]() ,
,![]() 所在抛物线的解析式为
所在抛物线的解析式为![]()
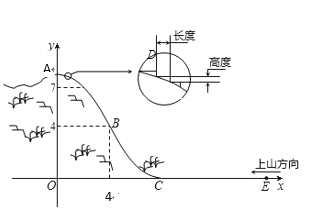
(1)求![]() 值,并写出山坡线
值,并写出山坡线![]() 的函数解析式;
的函数解析式;
(2)在山坡上的700米高度(点![]() )处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点
)处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点![]() 处,
处,![]() (米),假设索道
(米),假设索道![]() 可近似地看成一段以
可近似地看成一段以![]() 为顶点、开口向上的抛物线
为顶点、开口向上的抛物线![]() 当索道在
当索道在![]() 上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
(3)为了便于旅游观景,拟从山顶开始、沿迎面山坡往山下铺设观景台阶,台阶每级的高度为20厘米,长度因坡度的大小而定,但不得少于20厘米,每级台阶的两端点在坡面上(见图).试求出前三级台阶的长度(精确到厘米),并判断这种台阶能否一直铺到山脚,简述理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量![]() 的性质
的性质![]() ,类比得到复数
,类比得到复数![]() 的性质
的性质![]() ;
;
③方程![]() 有两个不同实数根的条件是
有两个不同实数根的条件是![]() 可以类比得到:方程
可以类比得到:方程![]() 有两个不同复数根的条件是
有两个不同复数根的条件是![]() ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义,其中类比错误的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各自独立地进行射击比赛,甲、乙两人向射击一次,击中目标的概率分别是![]() 和
和![]() ,假设每次射击是否击中目标相互之间没有影响.
,假设每次射击是否击中目标相互之间没有影响.
(1)求甲射击3次,至少有1次未击中目标的概率;
(2)求两人各射击3次,甲恰好击中目标2次且乙恰好击中目标1次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,SF快递收取快递费的标准是:重量不超过1kg的包裹收费10元;重量超过1kg的包裹,在收费10元的基础上,每超过1kg(不足1kg,按1kg计算)需再收5元.某县SF分代办点将最近承揽的100件包裹的重量统计如下:
重量(单位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件数 | 43 | 30 | 15 | 8 | 4 |
对近60天,每天揽件数量统计如下表:
件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件数 | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 1 | 6 |
以上数据已做近似处理,将频率视为概率.
(1)计算该代办未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com