
【题目】已知定义在[e,+∞)上的函数f(x)满足f(x)+xlnxf′(x)<0且f(2018)=0,其中f′(x)是函数![]() 的导函数,e是自然对数的底数,则不等式f(x)>0的解集为( )
的导函数,e是自然对数的底数,则不等式f(x)>0的解集为( )
A. [e,2018) B. [2018,+∞) C. (e,+∞) D. [e,e+1)
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
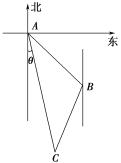
【题目】如图,甲船在A处,乙船在A处的南偏东45°方向,距A有9海里的B处,并以20海里每小时的速度沿南偏西15°方向行驶,若甲船沿南偏东θ度的方向,并以28海里每小时的速度行驶,恰能在C处追上乙船.问用多少小时追上乙船,并求sin θ的值.(结果保留根号,无需求近似值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的帮圆C经过点M(2,1),N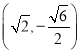 .
.
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,当△AMB面积取得最大值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员,甲投篮一次命中的概率为![]() ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为![]() ,若甲、乙各投篮三次,设
,若甲、乙各投篮三次,设![]() 为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
(1)若甲、乙第一次投篮都命中,求甲获胜(甲投篮命中数比乙多)的概率;
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义空间点到几何图形的距离为:这一点到这个几何图形上各点距离中最短距离.
(1)在空间,求与定点![]() 距离等于1的点所围成的几何体的体积和表面积;
距离等于1的点所围成的几何体的体积和表面积;
(2)在空间,线段![]() (包括端点)的长等于1,求到线段
(包括端点)的长等于1,求到线段![]() 的距离等于1的点所围成的几何体的体积和表面积;
的距离等于1的点所围成的几何体的体积和表面积;
(3)在空间,记边长为1的正方形![]() 区域(包括边界及内部的点)为
区域(包括边界及内部的点)为![]() ,求到
,求到![]() 距离等于1的点所围成的几何体的体积和表面积.
距离等于1的点所围成的几何体的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年中各月份的收入、支出情况的统计如图所示,下列说法中正确的是______.
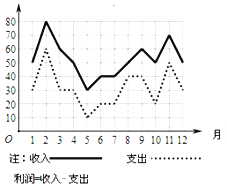
①2至3月份的收入的变化率与11至12月份的收入的变化率相同;
②支出最高值与支出最低值的比是6:1;
③第三季度平均收入为50万元;
④利润最高的月份是2月份。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com