
【题目】数列![]() 分别满足:
分别满足:![]() ,其中
,其中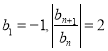 ,其中
,其中![]() ,设数列
,设数列![]() 前n项和分别为
前n项和分别为![]() .
.
(1)若数列![]() 为递增数列,求数列
为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:存在唯一的正整数k(
满足:存在唯一的正整数k(![]() ),使得
),使得![]() ,则称
,则称![]() 为“k坠点数列”
为“k坠点数列”
(Ⅰ)若数列![]() 为“6坠点数列",求
为“6坠点数列",求![]() ;
;
(Ⅱ)若数列![]() 为“5坠点数列”,是否存在“p坠点数列”
为“5坠点数列”,是否存在“p坠点数列”![]() ,使得
,使得![]() ,若存在,求正整数m的最大值;若不存在,说明理由.
,若存在,求正整数m的最大值;若不存在,说明理由.
【答案】(1)![]() ,
,![]() ;(2)(Ⅰ)
;(2)(Ⅰ)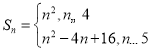 ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(1)由两数列为递增数列,结合递推式可得![]() ,
,![]() ,
,![]() ,
,![]() ,由此可得数列
,由此可得数列![]() 为等差数列,数列
为等差数列,数列![]() 从第二项起构成等比数列,然后利用等差数列和等比数列的通项公式求得答案;
从第二项起构成等比数列,然后利用等差数列和等比数列的通项公式求得答案;
(2)(Ⅰ)根据题目条件判断:数列![]() 必为1,3,5,7,5,7,9,11,
必为1,3,5,7,5,7,9,11,![]() ,即前4项为首项为1,公差为2的等差数列,从第5项开始为首项5,公差为2的等差数列,求解
,即前4项为首项为1,公差为2的等差数列,从第5项开始为首项5,公差为2的等差数列,求解![]() 即可.
即可.
(Ⅱ)运用数列![]() 为“坠点数列”且
为“坠点数列”且![]() ,综合判断数列
,综合判断数列![]() 中有且只有两个负项.假设存在正整数
中有且只有两个负项.假设存在正整数![]() ,使得
,使得![]() ,显然
,显然![]() ,且
,且![]() 为奇数,而
为奇数,而![]() 中各项均为奇数,可得
中各项均为奇数,可得![]() 必为偶数.再讨论
必为偶数.再讨论![]() ,
,![]() ,
,![]() ,证明
,证明![]() ,求出数列即可.
,求出数列即可.
解:(1)![]() 数列
数列![]() ,
,![]() 都为递增数列,
都为递增数列,
![]() 由递推式可得
由递推式可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则数列![]() 为等差数列,数列
为等差数列,数列![]() 从第二项起构成等比数列.
从第二项起构成等比数列.
![]() ,
,![]() ;
;
(2)(Ⅰ)![]() 数列
数列![]() 满足:存在唯一的正整数
满足:存在唯一的正整数![]() ,使得
,使得![]() ,且
,且![]() ,
,
![]() 数列
数列![]() 必为1,3,5,7,5,7,9,11,
必为1,3,5,7,5,7,9,11,![]() ,
,
即前4项为首项为1,公差为2的等差数列,从第5项开始为首项5,公差为2的等差数列,
故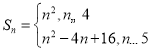 ;
;
(Ⅱ)![]() ,即
,即![]() ,
,
![]() ,
,
而数列![]() 为“
为“![]() 坠点数列”且
坠点数列”且![]() ,
,
![]() 数列
数列![]() 中有且只有两个负项.
中有且只有两个负项.
假设存在正整数![]() ,使得
,使得![]() ,显然
,显然![]() ,且
,且![]() 为奇数,
为奇数,
而![]() 中各项均为奇数,
中各项均为奇数,
![]() 必为偶数.
必为偶数.
由![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,故不存在正整数
,故不存在正整数![]() 使得
使得![]() ;
;
当![]() 时,
时,![]() ,
,
显然不存在正整数![]() 使得
使得![]() ;
;
当![]() 时,
时,![]() .
.
当![]() ,才存在正整数
,才存在正整数![]() 使得
使得![]() ;
;
即![]() .
.
当![]() 时,
时,![]() ,
,
构造:![]() 为1,3,1,3,5,7,9,
为1,3,1,3,5,7,9,![]() ,
,![]() 为
为![]() ,2,4,8,
,2,4,8,![]() ,32,64,
,32,64,![]()
此时![]() ,
,![]() .
.
![]() ,对应的
,对应的![]() ,
,![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】某面包推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:

(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(ⅰ)若日需求量为15个,求![]() ;
;
(ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: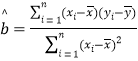
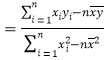 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
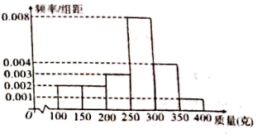
(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠DAB=90°AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC![]() ,E是线段AB的中点.
,E是线段AB的中点.
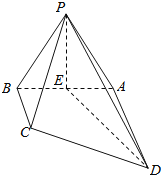
(1)求证:PE⊥CD;
(2)求PC与平面PDE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据《人民网》报道,“美国国家航空航天局( NASA)发文称,相比20年前世界变得更绿色了,卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的420/0来自于植树造林,下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
按造林方式分 | ||||||
地区 | 造林总面积 | 人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 |
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 221117 | 15376 | 133 |
重庆 | 226333 | 100600 | 、 62400 | 63333 | ||
陕西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012、 | 4000 | 3999 | 1053 | |
(1)请根据上述数据,分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(2)在这十个地区中,任选一个地区,求该地区人工造林面积与造林总面积的比值不足50%的概率是多少?
(3)从上表新封山育林面积超过十万公顷的地区中,任选两个地区,求至少有一个地区退化林修复面积超过五万公顷的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
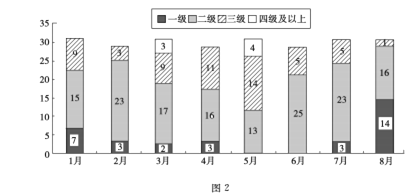
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,x轴的正半轴为极轴,建立坐标系,两个坐标系取相同的单位长度.已知直线
为极点,x轴的正半轴为极轴,建立坐标系,两个坐标系取相同的单位长度.已知直线![]() 的参数方程为
的参数方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程
的直角坐标方程
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,
两点,![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,若函数
,若函数![]() 满足:
满足:![]() ,都有
,都有![]() ,就称这个函数是点A的“限定函数”.以下函数:①
,就称这个函数是点A的“限定函数”.以下函数:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中是原点O的“限定函数”的序号是______.已知点
,其中是原点O的“限定函数”的序号是______.已知点![]() 在函数
在函数![]() 的图象上,若函数
的图象上,若函数![]() 是点A的“限定函数”,则实数a的取值范围是______.
是点A的“限定函数”,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴两端点与左焦点围成的三角形面积为3,短轴两端点与长轴一端点围成的三角形面积为2,设椭圆
的短轴两端点与左焦点围成的三角形面积为3,短轴两端点与长轴一端点围成的三角形面积为2,设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 是椭圆
是椭圆![]() 上除
上除![]() 两点外一动点.
两点外一动点.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左焦点作平行于直线
的左焦点作平行于直线![]() (
(![]() 是坐标原点)的直线
是坐标原点)的直线![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,求证:
,求证:![]() 成等比数列.
成等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com