
【题目】某总公司在A,B两地分别有甲、乙两个下属公司同时生产某种新能源产品(这两个公司每天都固定生产50件产品),所生产的产品均在本地销售.产品进入市场之前需要对产品进行性能检测,得分低于80分的定为次品,需要返厂再加工;得分不低于80分的定为正品,可以进入市场.检测员统计了甲、乙两个下属公司100天的生产情况及每件产品盈利亏损情况,数据如下表所示:
表1:
甲公司 | 得分 |
|
|
|
|
|
件数 | 10 | 10 | 40 | 40 | 50 | |
天数 | 10 | 10 | 10 | 10 | 80 |
表2:
乙公司 | 得分 |
|
|
|
| |
件数 | 10 | 5 | 40 | 45 | 50 | |
天数 | 20 | 10 | 20 | 10 | 70 |
表3:
每件正品 | 每件次品 | |
甲公司 | 盈2万元 | 亏3万元 |
乙公司 | 盈3万元 | 亏3.5万元 |
(1)分别求甲、乙两个公司这100天生产的产品的正品率(用百分数表示);
(2)试问甲乙两个公司这100天生产的产品的总利润哪个更大?说明理由.
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.

记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的四个顶点围成的菱形的面积为
的四个顶点围成的菱形的面积为![]() ,椭圆的一个焦点为
,椭圆的一个焦点为![]() .
.
(1)求椭圆的方程;
(2)若![]() ,
,![]() 为椭圆上的两个动点,直线
为椭圆上的两个动点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,当
,当![]() 时,
时,![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着疫情的有效控制,人们的生产生活逐渐向正常秩序恢复,位于我区的某著名赏花园区重新开放.据统计硏究,近期每天赏花的人数大致符合以下数学模型![]() .以
.以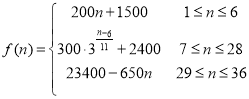 表示第
表示第![]() 个时刻进入园区的人数,以
个时刻进入园区的人数,以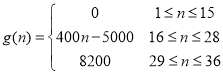 表示第
表示第![]() 个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即
个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即![]() 点30分作为第2个计算单位,即
点30分作为第2个计算单位,即![]() :依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
:依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
(1)试分别计算当天12:30至13:30这一小时内,进入园区的人数![]() 和离开园区的游客人数
和离开园区的游客人数![]() .
.
(2)请问,从12点(即![]() )开始,园区内总人数何时达到最多?并说明理由
)开始,园区内总人数何时达到最多?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“难度系数”反映试题的难易程度,难度系数越大,题目得分率越高,难度也就越小.“难度系数”的计算公式为![]() ,其中,
,其中,![]() 为难度系数,
为难度系数,![]() 为样本平均失分,
为样本平均失分,![]() 为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度系数 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
测试后,随机抽取了50名学生的数据进行统计,结果如下:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
实测平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根据试卷2的难度系数估计这480名学生第2套试卷的平均分;
(2)从抽样的50名学生的5套试卷中随机抽取2套试卷,记这2套试卷中平均分超过96分的套数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试卷的预估难度系数和实测难度系数之间会有偏差.设![]() 为第
为第![]() 套试卷的实测难度系数,并定义统计量
套试卷的实测难度系数,并定义统计量![]() ,若
,若![]() ,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,右准线为
,右准线为![]() .过点
.过点![]() 作与坐标轴都不垂直的直线与椭圆
作与坐标轴都不垂直的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
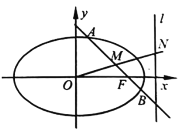
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得
,使得![]() 恒成立?若存在,求实数
恒成立?若存在,求实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有一块半径为R的扇形AOB公园,其中O为扇形所在圆的圆心,AOB=![]() ,OA,OB,
,OA,OB,![]() 为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在
为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在![]() 上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=
上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=![]() .
.

(1)如何设计,才能使市民从点O出发沿道路OM,MN行走至点N所经过的路径最长?请说明理由;
(2)如何设计,才能使市民从点A出发沿道路![]() ,MN行走至点N所经过的路径最长?请说明理由.
,MN行走至点N所经过的路径最长?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com