
分析 (Ⅰ)求出函数f(x)的定义域(0,+∞),求出函数的$f'(x)={e^{x-1}}-\frac{1}{x}$,求出切线的斜率,然后求解切线方程.
(Ⅱ)判断当x>1时,当0<x<1时,导函数的符号,判断函数的最小值位置,然后求解即可.
(Ⅲ)不等式恒成立转化为:$1+lnx>\frac{k(x-1)}{x}$,即$h(x)=\frac{x+xlnx}{x-1}>k$恒成立,即h(x)的最小值大于k,求出函数的导数,通过记g(x)=x-2-lnx,判断函数的最值,当x>a时,判断h'(x)符号,求解函数的最小值,可得正整数k的最大值.
解答 解:(Ⅰ)f(x)的定义域(0,+∞)),----------------------------------(1分)
由$f'(x)={e^{x-1}}-\frac{1}{x}$,$f'(1)={e^{1-1}}-\frac{1}{1}\;\;=1-1=0$,-------------(2分)
所以x=1处的切线垂直于y轴,且f(1)=1,--------------------(3分)
即切线l的方程为y=1.-----------------------(4分)
(Ⅱ)由$f'(x)={e^{x-1}}-\frac{1}{x}$,当x>1时f'(x)>0,-------------------------------(5分)
当0<x<1时f'(x)<0,------------------------------------------------(6分)
故f(x)在x=1时,f(x)取最小值,---------------------------------(7分)
最小值f(1)=1.---------------------------------(8分)
(Ⅲ)由${e^{x-1}}+1-f(x)>\frac{k(x-1)}{x}$,即$1+lnx>\frac{k(x-1)}{x}$,
即$h(x)=\frac{x+xlnx}{x-1}>k$恒成立.----------------------------(9分)
即h(x)的最小值大于k.---------------------------(10分)
$h'(x)=\frac{x-2-lnx}{{{{(x-1)}^2}}}>k$,
记g(x)=x-2-lnx,
则当x∈(1,+∞)时$g'(x)=\frac{x-1}{x}>0$,
所以,g(x)在(1,+∞)上单调递增,-----------------------(11分)
又g(3)=1-ln3<0,g(4)=2-ln4>0
∴g(x)=0存在唯一实根a,
且满足a∈(3,4),g(a)=a-2-lna=0,a=2+lna,---------------------(12分)
当x>a时,g(x)>0,h'(x)>0,当1<x<a时,g(x)<0,h'(x)<0,------(13分)
所以,$h{(x)_{min}}=h(a)=\frac{a+alna}{a-1}=\frac{a+a(a-2)}{a-1}=a∈(3,4)$,
故正整数k的最大值是3.------------------------------------(14分)
点评 本题考查函数的导数的综合应用,二次求导,构造法以及转化思想的应用,考查分类讨论思想的应用,难度比较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}+\frac{1}{2}i$ | B. | $\frac{1}{2}+i$ | C. | $\frac{1}{4}-\frac{1}{2}i$ | D. | $\frac{1}{2}-i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
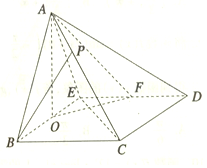 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
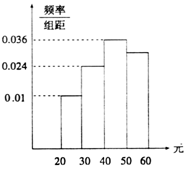 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )| A. | 10 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\frac{{5\sqrt{21}}}{7}$ | D. | $3\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1) | B. | (1)(2) | C. | (1)(3) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0,-4 | B. | $\frac{4}{27}$,-4 | C. | $\frac{4}{27}$,0 | D. | 2,0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com