分析:(1)此题由题意画出图形因为ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1为A1C1与B1D1的交点,且设AB1与底面A1B1C1D1所成角的大小为α,二面角A-B1D1-A1的大小为β,所以应先利用线面角及二面角的定义求出α,β,即可得证;
(2)由图形借助面面垂直找到点C在平面AB1D1的位置,利用三角形的相似解出.
解答:解:(1)由题意画出图形为:
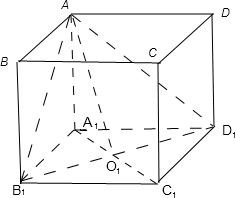
∵ABCD-A
1B
1C
1D
1是底面边长为1的正四棱柱,
∴底面为正方形且边长为1,又因为AB
1与底面A
1B
1C
1D
1所成角的大小为α,∴
∠AB1A1=α ,tanα=,
又因为二面角A-B
1D
1-A
1的大小为β,且底面边长为1的正四棱柱,O
1为A
1C
1与B
1D
1的交点,∴∠AO
1A
1=β,∴
tanβ= 而底面A
1B
1C
1D
1为边长为1的正方形,∴
A1B1= A1O1,∴
tanβ=tanα.
(2)∵O
1为B
1D
1的中点,而△AB
1D
1是以B
1D
1为底边的等腰三角形,∴AO
1⊥B
1D
1∴B
1D
1⊥平面ACC
1A
1∴平面AB
1D
1⊥平面ACC
1A
1且交线为AO
1,∴点C到平面AB
1D
1的投影点必落在A0
1上即垂足H,在矩形AA
1C
1C中,利用R
t△AA
1O
1∽R
t△CHA 得到
=,而
AH==,∴
=?
=?AA
1=2,
故正四棱锥的高为AA
1=2.
点评:此题重点考查了线面角,二面角,点到面的距离这些定义,还考查了学生的空间想象能力及计算能力.

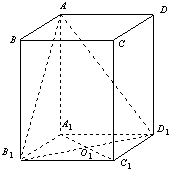 已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1为A1C1与B1D1的交点.
已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1为A1C1与B1D1的交点.


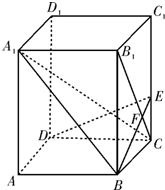 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,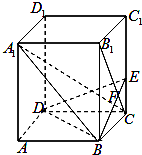 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.