练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了让居民了解垃圾分类，养成垃圾分类的习惯，让绿色环保理念深入人心．某市将垃圾分为四类：可回收物，餐厨垃圾，有害垃圾和其他垃圾．某班按此四类由10位同学组成四个宣传小组，其中可回收物与餐厨垃圾宣传小组各有2位同学，有害垃圾与其他垃圾宣传小组各有3位同学．现从这10位同学中选派5人到某小区进行宣传活动，则每个宣传小组至少选派1人的概率为（ ）

    A.B.C.D.

    【答案】C

    【解析】

    由题意计算出总情况数和符合要求的情况数，利用古典概型概率公式即可得解.

    将这10位同学中选派5人到某小区进行宣传活动共有种情况；

    每个宣传小组至少选派1人分为以下几种情况：

    ①可回收物或餐厨垃圾宣传小组选派两人，其他组每组一人，共有种情况；

    ②有害垃圾或其他垃圾宣传小组选派两人，其他组每组一人，共有种情况；

    故所求概率.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校高三（1）班在一次语文测试结束后，发现同学们在背诵内容方面失分较为严重.为了提升背诵效果，班主任倡议大家在早、晚读时间站起来大声诵读，为了解同学们对站起来大声诵读的态度，对全班50名同学进行调查，将调查结果进行整理后制成下表：

    考试分数

    频数

    5

    10

    15

    5

    10

    5

    赞成人数

    4

    6

    9

    3

    6

    4

    （1）欲使测试优秀率为30%，则优秀分数线应定为多少分？

    （2）依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系，列出2×2列联表，并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.

    参考公式及数据：，.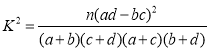

    0.100

    0.050

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若存在两个极值点，且关于的方程恰有三个实数根，，，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线的焦点为，准线为，为过焦点且垂直于轴的抛物线的弦，已知以为直径的圆经过点.

    （1）求的值及该圆的方程；

    （2）设为上任意一点，过点作的切线，切点为，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若是的极值点，求a的值及的单调区间；

    （2）若对任意，不等式成立，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于无穷数列，，记，，若同时满足条件①，均单调递增；②且，则称，是无穷互补数列.

    （1）若，，试判断数列，是否为无穷互补数列，并说明理由；

    （2）若，且，是无穷互补数列，求数列前项的和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．（是自然对数的底数）

    （1）求的单调递减区间；

    （2）记，若，试讨论在上的零点个数．（参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某品种一批树苗生长情况，在该批树苗中随机抽取了容量为120的样本，测量树苗高度(单位：cm)，经统计，其高度均在区间[19，31]内，将其按[19，21)，[21，23)，[23，25)，[25，27)，[27，29)，[29，31]分成6组，制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.

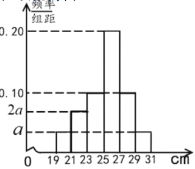
    （1）求图中a的值，并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表)；

    （2）已知所抽取的这120棵树苗来自于AB两个试验区，部分数据如下列联表：将列联表补充完整，并判断是否有99.9%的把握认为优质树苗与A，B两个试验区有关系，并说明理由.

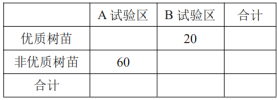
    参考数据：

    参考公式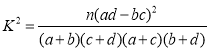：，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax3﹣（3a﹣2）x2﹣8x+12a+7，g（x）=lnx，记h（x）=min{f（x），g（x）}，若h（x）至少有三个零点，则实数a的取值范围是( )

    A.（﹣∞，）B.（，+∞）C.[，）D.[，]

    查看答案和解析>>

    同步练习册答案