
(08年福建卷理)(本小题满分12分)
如图,在四棱锥![]() 中,则面PAD⊥底面
中,则面PAD⊥底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]()
![]() ,
,![]() ,O为
,O为![]() 中点。
中点。
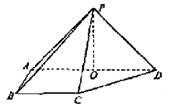
(Ⅰ)求证:PO⊥平面![]() ;
;
(Ⅱ)求异面直线PB与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解析:
解法一:
(Ⅰ)证明:在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD,平面![]() 平面ABCD=AD,
平面ABCD=AD,![]() 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
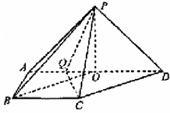
(Ⅱ)连结BO,在直角梯形ABCD中,BC∥AD,![]() ,
,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,所以OB∥DC.
由(Ⅰ)知,PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为![]() ,
,
在Rt△AOB中,AB=1,AO=1,
所以OB=![]() ,
,
在Rt△POA中,因为AP=![]() ,AO=1,所以OP=1,
,AO=1,所以OP=1,
在Rt△PBO中,tan∠PBO=![]()
所以异面直线PB与CD所成的角是![]() .
.
(Ⅲ)假设存在点Q,使得它到平面PCD的距离为![]() .
.
设![]() ,则
,则![]() ,由(Ⅱ)得CD=OB=
,由(Ⅱ)得CD=OB=![]() ,
,
在Rt△POC中, ![]()
所以PC=CD=DP, ![]()
由![]() 得
得![]() ,解得
,解得![]() ,
,
所以存在点Q满足题意,此时![]() .
.
解法二:
(Ⅰ)同解法一.
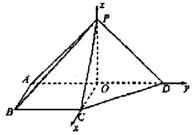
(Ⅱ)以![]() 为坐标原点,
为坐标原点,![]() 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系![]() ,依题意,易得
,依题意,易得![]() ,
,
所以![]()
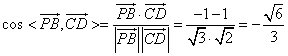 .
.
所以异面直线![]() 与
与![]() 所成的角是
所成的角是![]() .
.
(Ⅲ)假设存在点![]() ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为![]() ,
,
由(Ⅱ)知![]()
设平面![]() 的法向量为
的法向量为![]() .
.
则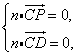 所以
所以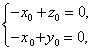 即
即![]() ,
,
取![]() ,得平面PCD的一个法向量为
,得平面PCD的一个法向量为![]() .
.
设![]() 由
由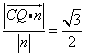 ,得
,得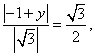
解![]() 或
或![]() (舍去),此时
(舍去),此时![]() ,
,
所以存在点Q满足题意,此时![]() .
.
【高考考点】本小题主要考查直线与平面位置关系、异面直线所成角、点到平面的距离等基本知识,考查空间想象能力、逻辑思维能力和运算能力。
【易错提醒】第一问就建立坐标系的就会导致错误.再者就是线与线所成角应该在![]() 才可
才可
【备考提示】因为立几的难度一再降低,所以一定要求学生掌握坐标法,劳记公式.


科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
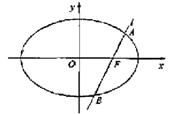
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科
目B的考试。已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书。现某人参加这项考试,科目A每次考试成绩合格的概率均为![]() ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为![]() .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为![]() ,求
,求![]() 的数学期望E
的数学期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
已知函数![]() .
.
(Ⅰ)设![]() 是正数组成的数列,前n项和为
是正数组成的数列,前n项和为![]() ,其中
,其中![]() .若点
.若点![]() (n∈N*)在函数
(n∈N*)在函数![]() 的图象上,求证:点
的图象上,求证:点![]() 也在
也在![]() 的图象上;
的图象上;
(Ⅱ)求函数![]() 在区间
在区间![]() 内的极值.
内的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
如图,在四棱锥![]() 中,则面PAD⊥底面
中,则面PAD⊥底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]()
![]() ,
,![]() ,O为
,O为![]() 中点。
中点。
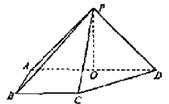
(Ⅰ)求证:PO⊥平面![]() ;
;
(Ⅱ)求异面直线PD与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com