
 ,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).
,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n). ,从而证得结论.
,从而证得结论. .
. .
. 的等比数列.
的等比数列. (a≠0,a,b,c是常数),
(a≠0,a,b,c是常数), ⑤,可得
⑤,可得 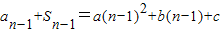 ⑥,
⑥, (a为非零常数).
(a为非零常数).

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:2012-2013学年浙江省杭州外国语高中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 ,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).
,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省徐州市高三(上)质量抽测数学试卷(解析版) 题型:解答题
 ,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).
,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏北四市高三(上)9月质量抽测数学试卷(解析版) 题型:解答题
 ,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).
,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省徐州市高三(上)9月质量检测数学试卷 (解析版) 题型:解答题
 ,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).
,其中c,c1,c2,…,ck为非零常数,数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=fk(n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com