
【题目】如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=![]() AC,AE=
AC,AE=![]() AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
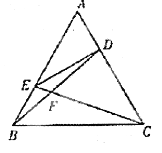
(Ⅰ)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
【答案】(1)证明过程详见解析;(2)![]() .
.
【解析】试题本题以正三角形为几何背景,考查四点共圆问题以及相似三角形问题,考查学生的转化与化归的能力.第一问,利用已知条件中边的比例关系可得出结论![]() ,再利用三角形相似,得出
,再利用三角形相似,得出![]() ,所以
,所以![]() ,所以可证
,所以可证![]() 四点共圆;第二问,根据所给正三角形的边长为2,利用已知的比例关系,得出各个小边的长度,从而得出
四点共圆;第二问,根据所给正三角形的边长为2,利用已知的比例关系,得出各个小边的长度,从而得出![]() 为正三角形,所以得出
为正三角形,所以得出![]() ,所以
,所以![]() 是
是![]() 所在圆的圆心,而
所在圆的圆心,而![]() 是半径,即为
是半径,即为![]() .
.
试题解析:(Ⅰ)证明:∵![]() , ∴
, ∴![]() ,
,
∵在正![]() 中,
中,![]() , ∴
, ∴![]() ,
,
又∵![]() ,
,![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
即![]() ,所以
,所以![]() 四点共圆. 5分
四点共圆. 5分
(Ⅱ)解:如图,
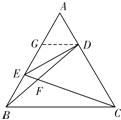
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∵![]() ,
,![]() , ∴
, ∴![]() 为正三角形,
为正三角形,
∴![]() ,即
,即![]() ,
,
所以点![]() 是
是![]() 外接圆的圆心,且圆
外接圆的圆心,且圆![]() 的半径为
的半径为![]() .
.
由于![]() 四点共圆,即
四点共圆,即![]() 四点共圆
四点共圆![]() ,其半径为
,其半径为![]() . 10分
. 10分


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中有![]() 个白球和
个白球和![]() 个红球(
个红球(![]() ,且
,且![]() ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含![]() 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率![]() ;
;
(2)若![]() ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为![]() ,当
,当![]() 为何值时,
为何值时,![]() 取最大值.
取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是_________.
(1)命题“若![]() ,则方程
,则方程![]() 有实数根”的逆否命题为“若方程
有实数根”的逆否命题为“若方程![]() 无实数根,则
无实数根,则![]() ”.
”.
(2)命题“![]() ,
,![]() ”的否定“
”的否定“![]() ,
,![]() ”.
”.
(3)若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题.
均为假命题.
(4)“![]() ”是“直线
”是“直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行”的充要条件.
平行”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
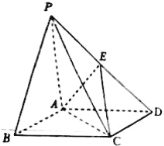
【题目】如图,在四棱锥P—ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC,PB=PD=![]() AC,E是PD的中点,求证:
AC,E是PD的中点,求证:
(1)PB∥平面ACE;
(2)平面PAC⊥平面ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是
分别是![]() 的中点,点
的中点,点![]() 在棱
在棱![]()
上, ![]() (
(![]() ).
).

(Ⅰ)三棱锥![]() 的体积分别为
的体积分别为![]() ,当
,当![]() 为何值时,
为何值时, ![]() 最大?最大值为多少?
最大?最大值为多少?
(Ⅱ)若![]() 平面
平面![]() ,证明:平面
,证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,
轴上,![]() 为椭圆
为椭圆![]() 短轴的一个端点,
短轴的一个端点,![]() 、
、![]() 为椭圆的左、右焦点,线段
为椭圆的左、右焦点,线段![]() 的延长线与椭圆
的延长线与椭圆![]() 相交于点
相交于点![]() ,且
,且![]() .
.
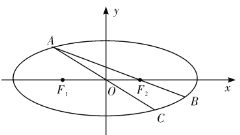
(1)求椭圆![]() 的方程;
的方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com