
分析 (1)若p∨q为真,则命题p,q存在真命题,分析求出两个命题为真时x的取值范围,进而可得答案;
(2)若¬p是¬q的必要不充分条件,则q是p的必要不充分条件,即p是q的充分不必要条件,进而可得答案;
解答 (本小题满分12分)
解:(1)若a=-1,
当p真时有1<x<3;…(2分)
又q真时有-6≤x<-3或2<x≤12…(4分)
由p∨q为真知,实数x的取值范围是[-6,-3)∪(1,12];…(6分)
(2)由?p是?q的必要不充分条件知,q是p的必要不充分条件,
∴p是q的充分不必要条件.…(8分)
若a>0,当p真时有-3a<x<-a;
∴-3a≥-6且-a≤-3;
无解;
若a<0,当p真时有-a<x<-3a;
∴-a≥2且-3a≤12;
∴-4≤a≤-2…(11分)
故实数a的取值范围是-4≤a≤-2…(12分)
点评 本题考查的知识点是命题的真假判断与应用,复合命题,充要条件,二次不等式的解法,难度中档.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
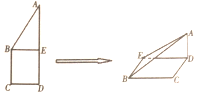 如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{4}$ | B. | $\frac{31}{4}$ | C. | $\frac{37-6\sqrt{3}}{4}$ | D. | $\frac{37-2\sqrt{33}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com