
 满足条件:
满足条件: =
= ,
, .
. 满足条件:
满足条件: =
= ,
, ,试判断四边形ABCD的形状,并给予证明.
,试判断四边形ABCD的形状,并给予证明.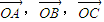 用三角形的各边对应的向量表示,得到边的关系,得出三角形的形状.
用三角形的各边对应的向量表示,得到边的关系,得出三角形的形状. ,根据向量的运算得出:∠AOB=∠COD;∠AOD=∠BOC从而∠AOD+∠COD=180°即A、O、C三点共线及、O、D三点共线,又
,根据向量的运算得出:∠AOB=∠COD;∠AOD=∠BOC从而∠AOD+∠COD=180°即A、O、C三点共线及、O、D三点共线,又 得出四边形ABCD为矩形.
得出四边形ABCD为矩形. (I)证明:设
(I)证明:设
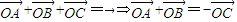


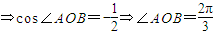 (3分)
(3分)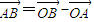

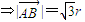
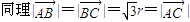
 ,则
,则 ⇒2r2+2r2cos∠AOB=2r2+2r2cos∠COD⇒∠AOB=∠COD
⇒2r2+2r2cos∠AOB=2r2+2r2cos∠COD⇒∠AOB=∠COD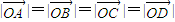


科目:高中数学 来源: 题型:
| F1F2 |
| PF1 |
| PF2 |
| A、椭圆 | B、圆 | C、直线 | D、线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OD |
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
| OD |
查看答案和解析>>
科目:高中数学 来源:0112 月考题 题型:解答题
 满足条件:
满足条件: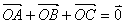 ,
,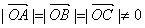 。
。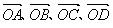 满足条件:
满足条件: ,
, ,试判断四边形ABCD的形状,并给予证明。
,试判断四边形ABCD的形状,并给予证明。 查看答案和解析>>
科目:高中数学 来源:2011年四川省内江市、广安市高考数学二模试卷(理科)(解析版) 题型:选择题
 |=2a(a>0),动点P与F1、F2在同一平面内,且满足|
|=2a(a>0),动点P与F1、F2在同一平面内,且满足| +
+ |=4a,则动点P的轨迹是( )
|=4a,则动点P的轨迹是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com