
分析 (1)此题可以按等量关系“每天的销售利润=(销售价-进价)×每天的销售量”列出函数关系式,并由售价大于进价,且销售量大于零求得自变量的取值范围.
(2)根据(1)所得的函数关系式,利用配方法求二次函数的最值即可得出答案.
解答 解:(1)由已知得每件商品的销售利润为(x-30)元,
那么m件的销售利润为y=m(x-30),
又m=162-3x.∴y=(x-30)(162-3x)=-3x2+252x-4860,30≤x≤54
(2)由(1)知对称轴为x=42,位于x的范围内,另抛物线开口向下,
∴当x=42时,${y_{max}}=-3×{42^2}+252×42-4860=432$,
∴当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.
点评 本题考查了二次函数在实际生活中的应用,解答本题的关键是根据等量关系:“每天的销售利润=(销售价-进价)×每天的销售量”列出函数关系式,另外要熟练掌握二次函数求最值的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19和2 | B. | 19和3 | C. | 19和4 | D. | 19和8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
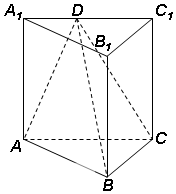 已知在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC⊥BC,BC=C1C=$\frac{1}{2}AC$=1,D是A1C1上的一点,且C1D=kA1C1.
已知在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC⊥BC,BC=C1C=$\frac{1}{2}AC$=1,D是A1C1上的一点,且C1D=kA1C1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com