
【题目】已知F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为
(a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F1的直线l交椭圆于A,B两点,当△ABF2面积最大时,求直线l的方程.
【答案】(Ⅰ)![]() y2=1;(Ⅱ)x﹣y
y2=1;(Ⅱ)x﹣y![]() 0或x+y
0或x+y![]() 0.
0.
【解析】
(Ⅰ)根据直线椭圆的过上顶点,得b=1,再利用点差法以及弦中点坐标解得a2=3,即得椭圆方程;
(Ⅱ)先设直线l方程并与椭圆方程联立,结合韦达定理,并以|F1F2|为底边长求△ABF2面积函数关系式,在根据基本不等式求△ABF2面积最大值,进而确定直线l的方程.
(Ⅰ)直线x+y=1与y轴的交于(0,1)点,∴b=1,
设直线x+y=1与椭圆C交于点M(x1,y1),N(x2,y2),
则x1+x2![]() ,y1+y2
,y1+y2![]() ,
,
∴![]() 1,
1,![]() 1,
1,
两式相减可得![]() (x1﹣x2)(x1+x2)
(x1﹣x2)(x1+x2)![]() (y1﹣y2)(y1+y2)=0,
(y1﹣y2)(y1+y2)=0,
∴![]() ,
,
∴![]()
![]()
![]() 1,
1,
解得a2=3,
∴椭圆C的方程为![]() y2=1.
y2=1.
(Ⅱ)由(Ⅰ)可得F1(![]() ,0),F2(
,0),F2(![]() ,0),设A(x3,y3),B(x4,y4),
,0),设A(x3,y3),B(x4,y4),
可设直线l的方程x=my![]() ,将直线l的方程x=my
,将直线l的方程x=my![]() 代入
代入![]() y2=1,可得(m2+3)y2﹣2
y2=1,可得(m2+3)y2﹣2![]() my﹣1=0,
my﹣1=0,
则y3+y4![]() ,y3y4
,y3y4![]() ,
,
|y3﹣y4|![]() ,
,
∴![]() |F1F2|
|F1F2|![]() |y3﹣y4|
|y3﹣y4|![]() |
|![]() |y3﹣y4|
|y3﹣y4|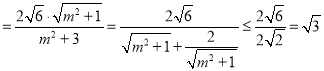 ,
,
当且仅当![]() ,即m=±1,△ABF2面积最大,
,即m=±1,△ABF2面积最大,
即直线l的方程为x﹣y![]() 0或x+y
0或x+y![]() 0.
0.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为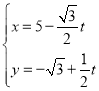 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为![]()
(1)求直线l和圆C的直角坐标方程;
(2)若点![]() 在圆C上,求
在圆C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人,让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民参与是打赢新型冠状病毒防疫战的根本方法.在防控疫情的过程中,某小区的“卡口”工作人员由“社区工作者”“下沉干部”“志愿者”三种身份的人员构成,其中社区工作者3人,下沉干部2人,志愿者1人.某电视台某天上午随机抽取2人进行访谈,某报社在该天下午随机抽取1人进行访谈.
(1)设![]() 表示上午抽到的社区工作者的人数,求随机变量
表示上午抽到的社区工作者的人数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)设![]() 为事件“全天抽到的
为事件“全天抽到的![]() 名工作人员的身份互不相同”,求事件
名工作人员的身份互不相同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为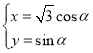 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,点
轴的正半轴为极轴,建立极坐标系,点![]() 的极坐标
的极坐标![]() ,直线
,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的标准参数方程;
的标准参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 的参数方程为
的参数方程为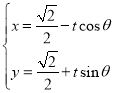 (t为参数),直线
(t为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市有东西南北四个进入城区主干道的人口,在早高峰时间段,时常发生交通拥堵,交警部门记录了11月份30天内的拥堵情况(如下表所示,其中●表示拥堵,○表示通畅).假设每个入口是否发生拥堵相互独立,将各入口在这30天内拥堵的频率代替各入口每天拥堵的概率.
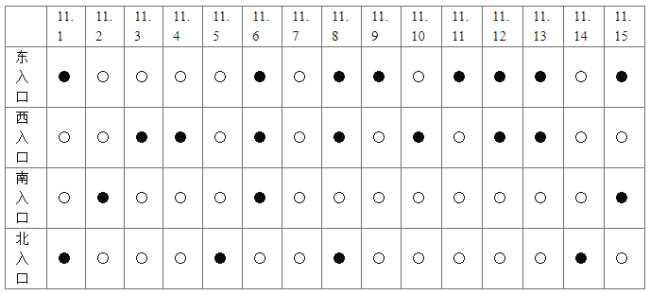
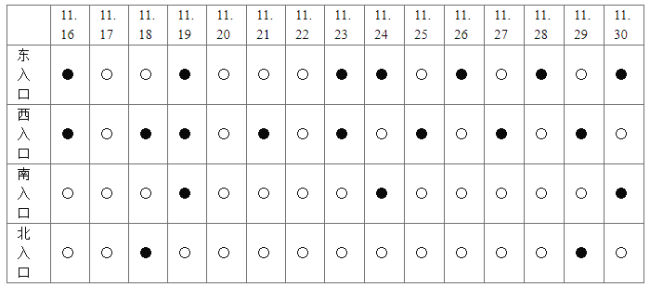
(1)分别求该城市一天中早高峰时间段这四个主干道的入口发生拥堵的概率.
(2)各入口一旦出现拥堵就需要交通协管员来疏通,聘请交通协管员有以下两种方案可供选择.方案一:四个主干道入口在早高峰时间段每天各聘请一位交通协管员,聘请每位交通协管员的日费用为m(![]() ,且
,且![]() )元.方案二:在早高峰时间段若某主干道入口发生拥堵,交警部门则需临时调派两位交通协管员协助疏通交通,调派后当日需给每位交通协管员的费用为200元.以四个主干道入口聘请交通协管员的日总费用的数学期望为依据,你认为在这两个方案中应该如何选择?请说明理由.
)元.方案二:在早高峰时间段若某主干道入口发生拥堵,交警部门则需临时调派两位交通协管员协助疏通交通,调派后当日需给每位交通协管员的费用为200元.以四个主干道入口聘请交通协管员的日总费用的数学期望为依据,你认为在这两个方案中应该如何选择?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图,给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出![]() 的值为( )
的值为( )
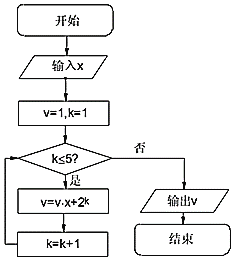
A.80B.192C.448D.36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com