
【题目】选修4—1:几何证明选讲
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.
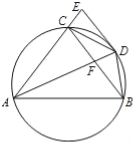
(1)求证:BC∥DE;
(2)若D、E、C、F四点共圆,且![]() ,求∠BAC.
,求∠BAC.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明直线平行,一般利用角的关系进行证明:由角平分线得∠DAC=∠DAB,再根据四点共圆得∠EDC=∠DAC,∠DAB=∠DCB,最后根据等量关系得证(2)由四点共圆得
∠CFA=∠CED,再由等弧对等角得∠CBA=∠BAC,因此在三角形ACF中,三个内角用∠DAC表示,解得∠BAC=2∠DAC ![]()
试题解析:(1)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
所以∠EDC=∠DCB,所以BC∥DE.…
(2)解:因为D,E,C,F四点共圆,所以∠CFA=∠CED
由(1)知∠ACF=∠CED,所以∠CFA=∠ACF.
设∠DAC=∠DAB=x,因为![]() ,所以∠CBA=∠BAC=2x,
,所以∠CBA=∠BAC=2x,
所以∠CFA=∠FBA+∠FAB=3x,
在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,则![]() ,所以∠BAC
,所以∠BAC![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】与均匀随机数特点不符的是( )
A. 它是[0,1]内的任何一个实数
B. 它是一个随机数
C. 出现的每一个实数都是等可能的
D. 是随机数的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-![]() .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,第二步归纳假设应写成( )
A.假设n=2k+1(k∈N*)正确,再推n=2k+3正确
B.假设n=2k﹣1(k∈N*)正确,再推n=2k+1正确
C.假设n=k(k∈N*)正确,再推n=k+1正确
D.假设n=k(k≥1)正确,再推n=k+2正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。为了更好的了解市民的态度,随机抽取了200人进行了调查,得到如下数据:
罚款金额 | 0 | 5 | 10 | 15 | 20 |
会继续乱扔垃圾的人数 | 80 | 50 | 40 | 20 | 10 |
(1)若乱扔垃圾的人数![]() 与罚款金额
与罚款金额![]() 满足线性回归方程,求回归方程
满足线性回归方程,求回归方程![]() ,其中
,其中![]() ,并据此分析,要使乱扔垃圾者不超过
,并据此分析,要使乱扔垃圾者不超过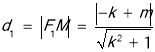 ,罚款金额至少是多少元?
,罚款金额至少是多少元?
(2)若以调查数据为基础,从5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业原有员工1000人,每人每年可为企业创利润15万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的2%,并且每年给每位待岗员工发放生活补贴1万元.据评估,当待岗员工人数![]() 不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润
不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润![]() 万元;当待岗员工人数
万元;当待岗员工人数![]() 超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
(1)求企业年利润![]() (万元)关于待岗员工人数
(万元)关于待岗员工人数![]() 的函数关系式
的函数关系式![]() ;
;
(2)为使企业年利润最大,应安排多少员工待岗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() (其中
(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 如图所示.
如图所示.
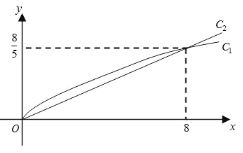
(1)求函数![]() 的解析式;
的解析式;
(2)若该商场一共投资8万元经销甲、乙两种商品,求该商场所获利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com