
【题目】已知椭圆![]() :
:![]() (
(![]() )经过点
)经过点![]() ,且两个焦点
,且两个焦点![]() ,
,![]() 的坐标依次为
的坐标依次为![]() 和
和![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,证明:直线
,证明:直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(Ⅰ)根据题意,由椭圆的定义可得
2a=![]() 计算可得a的值,由椭圆的几何性质可得b的值,将a、b的值代入椭圆的方程可得答案;
计算可得a的值,由椭圆的几何性质可得b的值,将a、b的值代入椭圆的方程可得答案;
(2)设直线EF的方程为y=kx+b,E(x1,y1),F(x2,y2),联立直线EF与椭圆方程,可得(3+4k2)x2+8kbx+4b2-12=0,分析可得(kx1+b)(kx2+b)=-x1x2,整理得(k2+1)x1x2+bk(x1+x2)+b2=0,由直线与圆的位置关系分析可得结论.
详解:
(1)由椭圆定义得![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
直线![]() 的方程与椭圆方程联立,消去
的方程与椭圆方程联立,消去![]() 得
得![]() ,
,
当![]() 时,得
时,得![]() ,
,![]() ,
,
由已知![]() ,即
,即![]() ,因为点
,因为点![]() ,
,![]() 在直线
在直线![]() 上,
上,
所以![]() ,整理得
,整理得![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() ,
,
所以直线与一个定圆相切,定圆的标准方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如列联表.
的概率分布如列联表.
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响求该企业在这两个月内共被消费者投诉![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,AD=DC=AP=2,AB=1,点E为棱PC的中点.
,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段![]() (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.

(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 其中P,M是非空数集.记f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
其中P,M是非空数集.记f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
(Ⅰ)若P=[0,3],M=(﹣∞,﹣1),求f(P)∪f(M);
(Ⅱ)若P∩M=,且f(x)是定义在R上的增函数,求集合P,M;
(Ⅲ)判断命题“若P∪M≠R,则f(P)∪f(M)≠R”的真假,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰直角三角形![]() 的斜边AB为正四面体
的斜边AB为正四面体![]() 侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下列说法:
侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下列说法:

(1)四面体E![]() BCD的体积有最大值和最小值;
BCD的体积有最大值和最小值;
(2)存在某个位置,使得![]() ;
;
(3)设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ;
;
(4)AE的中点M与AB的中点N连线交平面BCD于点P,则点P的轨迹为椭圆.
其中,正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脐橙营养丰富,含有人体所必需的各类营养成份,若规定单个脐橙重量(单位:千克)在[0.1,0.3)的脐橙是“普通果”,重量在[0.3,0.5)的磨橙是“精品果”,重量在[0.5,0.7]的脐橙是“特级果”,有一果农今年种植脐橙,大获丰收为了了解脐橙的品质,随机摘取100个脐橙进行检测,其重量分别在[0.1,0.2),[0.2,0.3),[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7]中,经统计得到如图所示频率分布直方图
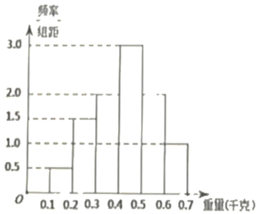
(1)将频率视为概率,用样本估计总体.现有一名消费者从脐橙果园中,随机摘取5个脐橙,求恰有3个是“精品果”的概率.
(2)现从摘取的100个脐橙中,采用分层抽样的方式从重量为[0.4,0.5),[0.5,0.6)的脐橙中随机抽取10个,再从这10个抽取3个,记随机变量X表示重量在[0.5,0.6)内的脐橙个数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四种说法:
(1)函数![]()
![]() 与函数
与函数![]()
![]() 的定义域相同;
的定义域相同;
(2)函数![]() 与
与![]() 的值域相同;
的值域相同;
(3)若函数![]() 式定义在R上的偶函数且在
式定义在R上的偶函数且在![]() 为减函数对于锐角
为减函数对于锐角![]() 则
则![]() ;
;
(4)若函数![]() 且
且![]()
![]() ,则
,则![]() ;
;
其中正确说法的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com