
分析 (Ⅰ)根据绝对值的意义求得(|x+1|+|x-5|)min,可得m的范围.
(Ⅱ)不等式等价于m+$\frac{9}{m}$≤6,当m<0时,上式成立; 当m>0时利用基本不等式可得m=3时,m+$\frac{9}{m}$≤6成立,综上可得实数m的取值范围.
解答 解:(Ⅰ)若函数$y=\sqrt{f(x)}$的定义域为R,则m≤|x+1|+|x-5|对x∈R恒成立,
所以m≤(|x+1|+|x-5|)min,又|x+1|+|x-5|≥|x+1-(x-5)|=6,所以m≤6,
即实数m的取值范围为(-∞,6].
(Ⅱ)$f(x)≥\frac{9}{m}$对任意的实数x恒成立$?|x+1|+|x-5|≥m+\frac{9}{m}$对任意的实数x恒成立,$?m+\frac{9}{m}≤6$,
当m<0时,上式成立; 当m>0时$m+\frac{9}{m}≥2\sqrt{m•\frac{9}{m}}=6$,当且仅当$m=\frac{9}{m}$,即m=3时上式取等号;
综上实数m的取值范围为(-∞,0)∪{3}.
点评 本题主要考查绝对值的意义,函数的恒成立问题,基本不等式的应用,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | π | B. | -1 | C. | 1 | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
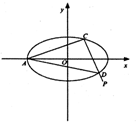 如图,在平面直角坐标系xOy中,A是椭圆G:$\frac{{x}^{2}}{4}$+y2=1的左顶点,过点P(2,-1)任意作一条直线l与椭圆G交于C,D,记直线AC,AD的斜率分别为k1,k2,则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$的值为-4.
如图,在平面直角坐标系xOy中,A是椭圆G:$\frac{{x}^{2}}{4}$+y2=1的左顶点,过点P(2,-1)任意作一条直线l与椭圆G交于C,D,记直线AC,AD的斜率分别为k1,k2,则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$的值为-4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{9}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
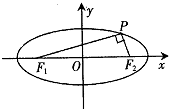 如图,P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=90°,则|PF1|•|PF2|等于( )
如图,P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=90°,则|PF1|•|PF2|等于( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com