
【题目】为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个![]() 列联表:
列联表:
认为作业多 | 认为作业不多 | 合计 | |
喜欢玩手机游戏 | 18 | 2 | |
不喜欢玩手机游戏 | 6 | ||
合计 | 30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(2)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(3)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
参考公式及参考数据:独立性检验概率表
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
计算公式: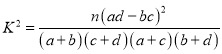
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥D—ABC的四个顶点在球O的球面上,若AB=AC=BC=DB=DC=1,当三棱锥D—ABC的体积取到最大值时,球O的表面积为( )
A. ![]() B. 2πC. 5πD.
B. 2πC. 5πD. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
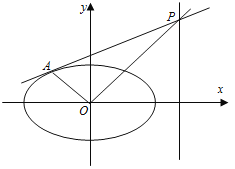
【题目】已知椭圆![]() ,点
,点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() ,切点为
,切点为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)若切线![]() 的斜率为1,求点
的斜率为1,求点![]() 的坐标;
的坐标;
(2)求![]() 的面积的最小值,并求出此时
的面积的最小值,并求出此时![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥S﹣ABC中,SA=SB=SC,∠ABC=90°,AB>BC,E,F,G分别是AB,BC,CA的中点,记直线SE与SF所成的角为α,直线SG与平面SAB所成的角为β,平面SEG与平面SBC所成的锐二面角为γ,则( )
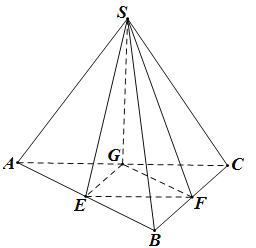
A.α>γ>βB.α>β>γC.γ>α>βD.γ>β>α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣2,1),B(2,4),点P是直线l:y=x上的动点.
(1)若PA⊥PB,求点P的坐标;
(2)设过A的直线l1与过B的直线l2均平行于l,求l1与l2之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣cosx,a≠0.
(1)若函数f(x)为单调函数,求a的取值范围;
(2)若x∈[0,2π],求:当a≥![]() 时,函数f(x)仅有一个零点.
时,函数f(x)仅有一个零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com