
设函数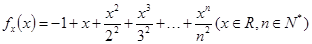 ,证明:
,证明:
(Ⅰ)对每个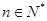 ,存在唯一的
,存在唯一的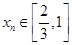 ,满足
,满足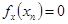 ;
;
(Ⅱ)对任意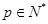 ,由(Ⅰ)中
,由(Ⅰ)中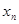 构成的数列
构成的数列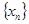 满足
满足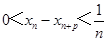 .
.
见解析
【解析】(1)对每个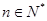 ,当
,当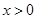 时,
时,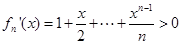 ,
,
则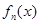 在
在 内单调递增,
内单调递增,
而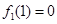 ,当
,当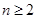 时,
时,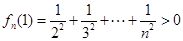 ,
,
故 ,
,
又
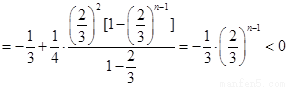
所以对每个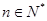 ,存在唯一的
,存在唯一的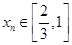 ,满足
,满足
当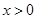 时,
时,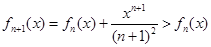 ,并由(1)知
,并由(1)知
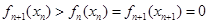
由 在
在 内单调递增知,
内单调递增知, ,故
,故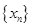 为单调递减数列,
为单调递减数列,
从而对任意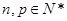 ,
,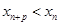
对任意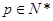 ,
,
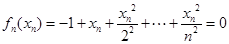 ①
①
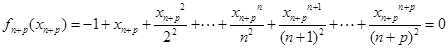 ②
②
①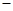 ②并移项,利用
②并移项,利用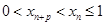 ,得
,得
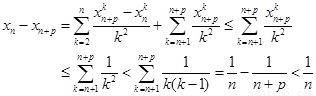
因此,对任意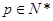 ,
,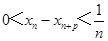 .
.
本题考查的是数列函数,而且含双变量,考生在做题的过程中需要冷静的处理好每个变量.第(1)题考查函数的零点问题,要证明对每个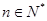 ,函数在某个区间上只有一个零点,一方面要证明函数是单调的,求导即可,另一方面要判断
,函数在某个区间上只有一个零点,一方面要证明函数是单调的,求导即可,另一方面要判断 的正负问题,此题难点在于判断
的正负问题,此题难点在于判断 的正负时,要利用放缩的思想,将这个数列函数放缩到可以利用等比数列求和,从而证明此函数在指定区间内只有一个零点;第(2)题要将数列从数列函数中分离出来,就要通过函数的单调性,由
的正负时,要利用放缩的思想,将这个数列函数放缩到可以利用等比数列求和,从而证明此函数在指定区间内只有一个零点;第(2)题要将数列从数列函数中分离出来,就要通过函数的单调性,由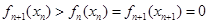 ,
, 在
在 内单调递增,确定
内单调递增,确定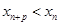 ,则不等式左半边成立,右半边通过作差,数列放缩确定最终
,则不等式左半边成立,右半边通过作差,数列放缩确定最终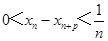 .本题属于较难题.
.本题属于较难题.
【考点定位】考查函数的导数及其应用,函数零点的判定,等比数列的求和,不等式的放缩等知识.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
(04年广东卷)(12分)
设函数![]()
(I)证明:当![]() 且
且![]() 时,
时,![]()
(II)点![]() (0<x0<1)在曲线
(0<x0<1)在曲线![]() 上,求曲线上在点
上,求曲线上在点![]() 处的切线与
处的切线与![]() 轴,
轴,![]() 轴正向所围成的三角形面积的表达式。(用
轴正向所围成的三角形面积的表达式。(用![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省高三上学期期中考试数学试卷(解析版) 题型:解答题
设函数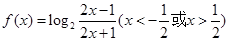 .
.
(1)证明: 是奇函数;
是奇函数;
(2)求 的单调区间;
的单调区间;
(3)写出函数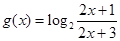 图象的一个对称中心.
图象的一个对称中心.
查看答案和解析>>
科目:高中数学 来源:2013届北京西城(南区)高二下学期期末考试理科数学试卷(解析版) 题型:解答题
(Ⅰ)设函数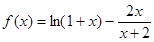 ,证明:当
,证明:当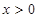 时,
时,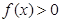 ;
;
(Ⅱ)从编号1到100的100张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取20次,设抽得的20个号码互不相同的概率为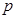 。证明:
。证明: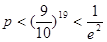 。
。
注:可用(Ⅰ)的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com