
【题目】为了了解游客的情况,以便制定相应的策略,在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如图:
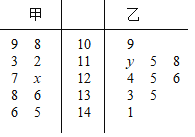
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为![]() ,求概率
,求概率![]() ;
;
(3)现从如图所示的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)分布列见解析,
;(3)分布列见解析,![]() .
.
【解析】
(1)10位数中位数为第5位和第6位数之和除以2,找出数值计算即可;
(2)由题意判断该分布符合二项分布,结合二项分布公式求解即可;
(3)由题分别求出景点甲中被选出的概率为![]() ,在景点乙中被选出的概率为
,在景点乙中被选出的概率为![]() ,判断知
,判断知![]() 的所有可能的取值为0,1,2,由相互独立事件的乘法公式计算求出对应概率,列出分布列,即可求出期望
的所有可能的取值为0,1,2,由相互独立事件的乘法公式计算求出对应概率,列出分布列,即可求出期望
(1)景点甲中的数据的中位数是125,可得![]()
![]() ,景点乙中的数据的平均数是124,可得
,景点乙中的数据的平均数是124,可得![]() ,解得
,解得![]() ;
;
(2)由题意知:因为景点甲的每一天的游客数超过120人的概率为![]() ,
,
任取4天,即是进行了4次独立重复试验,其中有![]() 次发生,
次发生,
故随机变量![]() 服从二项分布,则
服从二项分布,则![]() ,
,
(3)从图中看出:景点甲的数据中符合条件的只有1天,景点乙的数据中符合条件的有4天,所以在景点甲中被选出的概率为![]() ,在景点乙中被选出的概率为
,在景点乙中被选出的概率为![]() .
.
由题意知:![]() 的所有可能的取值为0,1,2.
的所有可能的取值为0,1,2.
则![]() ,
,
所以得分布列为:
| 0 | 1 | 2 |
P |
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】对于正整数![]() ,如果
,如果![]() 个整数
个整数![]() 满足
满足![]() ,
,
且![]() ,则称数组
,则称数组![]() 为
为![]() 的一个“正整数分拆”.记
的一个“正整数分拆”.记![]() 均为偶数的“正整数分拆”的个数为
均为偶数的“正整数分拆”的个数为![]() 均为奇数的“正整数分拆”的个数为
均为奇数的“正整数分拆”的个数为![]() .
.
(Ⅰ)写出整数4的所有“正整数分拆”;
(Ⅱ)对于给定的整数![]() ,设
,设![]() 是
是![]() 的一个“正整数分拆”,且
的一个“正整数分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)对所有的正整数![]() ,证明:
,证明:![]() ;并求出使得等号成立的
;并求出使得等号成立的![]() 的值.
的值.
(注:对于![]() 的两个“正整数分拆”
的两个“正整数分拆”![]() 与
与![]() ,当且仅当
,当且仅当![]() 且
且![]() 时,称这两个“正整数分拆”是相同的.)
时,称这两个“正整数分拆”是相同的.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯将于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传国际篮联篮球世界杯,某大学从全校学生中随机抽取了120名学生,对是否会收看该国际篮联篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关?
(2)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() .
.
(i)求乙投球的命中率![]() ;
;
(ii)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: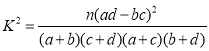 ,其中
,其中![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了100名高中生,根据问卷调查,得到以下数据:
作文成绩优秀 | 作文成绩一般 | 总计 | |
课外阅读量较大 | 35 | 20 | 55 |
课外阅读量一般 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.5%的把握认为课外阅读量的大小与作文成绩优秀有关;
(2)若用分层抽样的方式从课外阅读量一般的高中生中选取了6名高中生,再从这6名高中生中随机选取2名进行面谈,求面谈的高中生中至少有1名作文成绩优秀的概率.
附: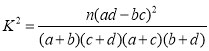 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节(每年农历五月初五),是中国传统节日,有吃粽子的习俗.某超市在端午节这一天,每售出![]() kg粽子获利润
kg粽子获利润![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg亏损
kg亏损![]() 元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了
元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了![]() kg粽子.以
kg粽子.以![]() (单位:kg,
(单位:kg,![]() )表示今年的市场需求量,
)表示今年的市场需求量,![]() (单位:元)表示今年的利润.
(单位:元)表示今年的利润.
市场需求量(kg) |
|
|
|
|
|
频率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)在频率分布表的市场需求量分组中,以各组的区间中间值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率
的频率![]() ),求
),求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com