
分析 (1)利用直接法,建立方程,即可求曲线C的方程.
(2)直线与圆的方程联立,求出A,B的坐标,利用斜率公式,即可证明直线BC的斜率为定值.
解答 解:(1)设曲线M上任意一点为Q(x,y),由题意得$\frac{{|{OQ}|}}{{|{AQ}|}}=\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{{{({x-3})}^2}+{{({y+6})}^2}}}}=\frac{1}{2}⇒{({x+1})^2}+{({y-2})^2}=20$,此即为曲线M的方程.
(2)由题意知,直线PB和直线PC的斜率存在,且互为相反数,故可设直线PB的方程为:y+2=k(x-1),
由$\left\{\begin{array}{l}y+2=k({x-1})\\{({x+1})^2}+{({y+2})^2}=20\end{array}\right.⇒({1+{k^2}}){x^2}+2({1-{k^2}-4k})x+{k^2}+8k-3=0$,
因为点P的横坐标x=1一定是该方程的解,故可得${x_B}=\frac{{{k^2}+8k-3}}{{1+{k^2}}}$,同理${x_C}=\frac{{{k^2}-8k-3}}{{1+{k^2}}}$(以-k为k),
所以${k_{BC}}=\frac{{{y_C}-{y_B}}}{{{x_C}-{x_B}}}=\frac{{-k({{x_C}-1})-k({{x_B}-1})}}{{{x_C}-{x_B}}}=\frac{{2k-k({{x_C}+{x_B}})}}{{{x_C}-{x_B}}}=-\frac{1}{2}$.
故直线BC的斜率为定值$-\frac{1}{2}$.
点评 本题考查轨迹方程,考查直线的斜率为定值的证明,考查学生的计算能力,是中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
下列四个命题:①一个命题的逆命题为真,则它的逆否命题一定为真;②命题“设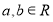 ,若
,若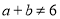 ,则
,则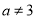 或
或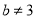 ”是一个假命题;③“
”是一个假命题;③“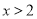 ”是“
”是“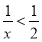 ”的充分不必要条件;④一个命题的否命题为真,则它的逆命题一定为真.其中不正确的命题是 .(写出所有不正确命题的序号)
”的充分不必要条件;④一个命题的否命题为真,则它的逆命题一定为真.其中不正确的命题是 .(写出所有不正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
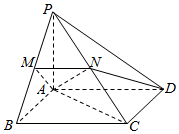 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M、N分别为线段PB,PC 上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M、N分别为线段PB,PC 上的点,MN⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
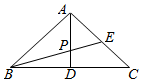 如图,等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,BE平分∠ABC,AD与BE交于点P,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ等于( )
如图,等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,BE平分∠ABC,AD与BE交于点P,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ等于( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com