
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)在(-∞,-1-![]() ),(-1+
),(-1+![]() ,+∞)单调递减,在(-1-
,+∞)单调递减,在(-1-![]() ,-1+
,-1+![]() )单调递增(2)[1,+∞)
)单调递增(2)[1,+∞)
【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号确定单调区间;(2)对![]() 分类讨论,当a≥1时,
分类讨论,当a≥1时,![]() ,满足条件;当
,满足条件;当![]() 时,取
时,取![]() ,当0<a<1时,取
,当0<a<1时,取![]() ,
,![]() .
.
试题解析: 解(1)f ’(x)=(1-2x-x2)ex
令f’(x)=0得x=-1-![]() ,x=-1+
,x=-1+![]()
当x∈(-∞,-1-![]() )时,f’(x)<0;当x∈(-1-
)时,f’(x)<0;当x∈(-1-![]() ,-1+
,-1+![]() )时,f’(x)>0;当x∈(-1-
)时,f’(x)>0;当x∈(-1-![]() ,+∞)时,f’(x)<0
,+∞)时,f’(x)<0
所以f(x)在(-∞,-1-![]() ),(-1+
),(-1+![]() ,+∞)单调递减,在(-1-
,+∞)单调递减,在(-1-![]() ,-1+
,-1+![]() )单调递增
)单调递增
(2) f (x)=(1+x)(1-x)ex
当a≥1时,设函数h(x)=(1-x)ex,h’(x)= -xex<0(x>0),因此h(x)在[0,+∞)单调递减,而h(0)=1,
故h(x)≤1,所以
f(x)=(x+1)h(x)≤x+1≤ax+1
当0<a<1时,设函数g(x)=ex-x-1,g’(x)=ex-1>0(x>0),所以g(x)在在[0,+∞)单调递增,而g(0)=0,故ex≥x+1
当0<x<1,![]() ,
,![]() ,取
,取![]()
则![]()
当 ![]()
综上,a的取值范围[1,+∞)
点睛:利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.


科目:高中数学 来源: 题型:
【题目】如图1,2,在Rt△ABC中,AB=BC=4,点E在线段AB上,过点E作交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°. 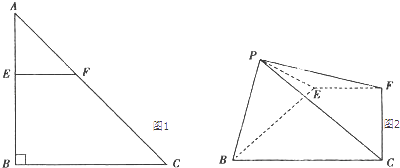
(1)求证:EF⊥PB;
(2)试问:当点E在何处时,四棱锥P﹣EFCB的侧面的面积最大?并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x+2)的定义域为(0,2),则函数y=f(log2x)的定义域为( )
A.(﹣∞,1)
B.(1,4)
C.(4,16)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cos A<cos B的充要条件
B.命题p:对任意的x∈R,x2+x+1>0,则¬p:对任意的x∈R,x2+x+1≤0
C.已知p: ![]() >0,则¬p:
>0,则¬p: ![]() ≤0
≤0
D.存在实数x∈R,使sin x+cos x= ![]() 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: (![]() >b>0)的离心率为
>b>0)的离心率为![]() ,A(
,A(![]() ,0), B(0,b),O(0,0),△OAB的面积为1.
,0), B(0,b),O(0,0),△OAB的面积为1.
(1)求椭圆C的方程;
(2)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN|·|BM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,并根据 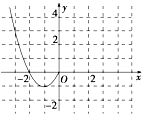
(1)写出函数f(x)(x∈R)的增区间;
(2)写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)﹣2ax+2(x∈[1,2]),求函数g(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,过原点分别作曲线
时,过原点分别作曲线![]() 与
与![]() 的切线
的切线![]() ,
, ![]() ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明: ![]() ;
;
(3)设![]() ,当
,当![]() ,
, ![]() 时,求实数
时,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com