
【题目】有着“中国碳谷”之称的安徽省淮北市,名优特产众多,其中“塔山石榴”因其青皮软籽、籽粒饱满、晶莹剔透、汁多味甘而享誉天下.现调查表明,石榴的甜度与海拔、日照时长、昼夜温差有着极强的相关性,分别用![]() 表示石榴甜度与海拔、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标
表示石榴甜度与海拔、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标![]() 的值评定石榴的等级,若
的值评定石榴的等级,若![]() 则为一级;若
则为一级;若![]() 则为二级;若
则为二级;若![]() 则为三级.
则为三级.![]() 近年来,周边各地市也开始发展石榴的种植,为了了解目前石榴在周边地市的种植情况,研究人员从不同地市随机抽取了12个石榴种植园,得到如下结果:
近年来,周边各地市也开始发展石榴的种植,为了了解目前石榴在周边地市的种植情况,研究人员从不同地市随机抽取了12个石榴种植园,得到如下结果:
种植园编号 | A | B | C | D | E | F |
|
|
|
|
|
|
|
种植园编号 | G | H | I | J | K | L |
|
|
|
|
|
|
|
(1)若有石榴种植园120个,估计等级为一级的石榴种植园的数量;
(2)在所取样本的二级和三级石榴种植园中任取2个,![]() 表示取到三级石榴种植园的数量,求随机变量
表示取到三级石榴种植园的数量,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: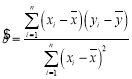 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
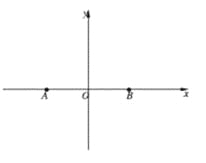
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名贫困户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“
级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“![]() 级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆E:
为椭圆E:![]() 的左、右焦点,过点
的左、右焦点,过点![]() 的直线l与椭圆E有且只有一个交点T.
的直线l与椭圆E有且只有一个交点T.
(1)求![]() 面积的取值范围.
面积的取值范围.
(2)若有一束光线从点![]() 射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝建国70周年,校园文化节举行有奖答题活动,现有A,B两种题型,从A类题型中抽取1道,从B类题型中抽取2道回答,答对3道题获新华书店面值为15元的图书代金券,答对2道题获面值为10元的图书代金券,答对1道题获面值为5元的图书代金券,没有答对获面值为1元的图书代金券(作为鼓励).甲同学参加此活动答对A类题的概率为![]() ,答对B类题的概率为
,答对B类题的概率为![]() .
.
(Ⅰ)求甲答对1道题的概率;
(Ⅱ)设甲参加一次活动所获图书代金券的面值为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,己知抛物线
中,己知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的一点,点
上的一点,点![]() 的坐标为
的坐标为![]()
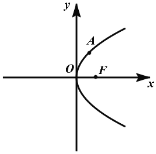
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)弦![]() 经过点
经过点![]() ,过弦
,过弦![]() 上一点
上一点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,求证:“直线
,求证:“直线![]() 与抛物线相切”的一个充要条件是“
与抛物线相切”的一个充要条件是“![]() 为弦
为弦![]() 的中点”.
的中点”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com