
【题目】设Sn是数列[an}的前n项和, ![]() .
.
(1)求{an}的通项;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】
(1)解:∵ ![]() ,
,
∴n≥2时, ![]() ,
,
展开化简整理得,Sn﹣1﹣Sn =2Sn﹣1Sn,∴ ![]() ,∴数列{
,∴数列{ ![]() }是以2为公差的等差数列,其首项为
}是以2为公差的等差数列,其首项为 ![]() .
.
∴ ![]() ,
, ![]() .
.
由已知条件 ![]() 可得
可得 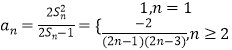 .
.
(2)解:由于 ![]() ,
,
∴数列{bn}的前n项和 ![]() ,
,
∴ ![]() .
.
【解析】(1)由条件可得n≥2时, ![]() ,整理可得
,整理可得 ![]() ,故数列{
,故数列{ ![]() }是以2为公差的等差数列,其首项为
}是以2为公差的等差数列,其首项为 ![]() ,由此求得sn . 再由
,由此求得sn . 再由 ![]() 求出{an}的通项公式.(2)由(1)知,
求出{an}的通项公式.(2)由(1)知, ![]() ,用裂项法求出数列{bn}的前n项和Tn .
,用裂项法求出数列{bn}的前n项和Tn .
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】口袋中装有一些大小相同的红球和黑球,从中取出2个球.两个球都是红球的概率是 ![]() ,都是黑球的概率是
,都是黑球的概率是 ![]() ,则取出的2个球中恰好一个红球一个黑球的概率是( )
,则取出的2个球中恰好一个红球一个黑球的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S表示所有大于﹣1的实数构成的集合,确定所有的函数:S→S,满足以下两个条件:
对于S内的所有x和y,f(x+f(y)+xf(y))=y+f(x)+yf(x);在区间﹣1<x<0与x>0的每一个内, ![]() 是严格递增的.求满足上述条件的函数的方程.
是严格递增的.求满足上述条件的函数的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差数列.
(1)求a1
(2)证明 ![]() 为等比数列,并求数列{an}的通项;
为等比数列,并求数列{an}的通项;
(3)设bn=log3(an+2n),且Tn= ![]() ,证明Tn<1.
,证明Tn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,a1=2,a3=18.数列{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{an},{bn}的通项公式;
(2)设Pn=b1+b4+b7+…+b3n﹣2 , Qn=b10+b12+b14+…+b2n+8 , 其中n=1,2,3,….试比较Pn与Qn的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
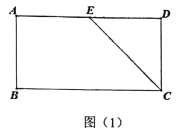
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
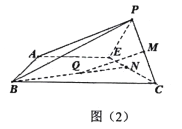
的位置,使![]() ,如图(2).
,如图(2).
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com