
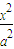 +
+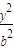 =1 (a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是
=1 (a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是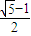 ,则∠ABF= .
,则∠ABF= . 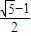 a,解出b2=a2-c2=
a,解出b2=a2-c2=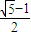 a2.在△ABF中分别计算出|AB|2、|BF|2和|AF|2,可得AF|2=|AB|2+|BF|2,所以△ABF是以AF为斜边的直角三角形,即∠ABF=90°.
a2.在△ABF中分别计算出|AB|2、|BF|2和|AF|2,可得AF|2=|AB|2+|BF|2,所以△ABF是以AF为斜边的直角三角形,即∠ABF=90°.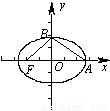 解:∵椭圆的离心率是
解:∵椭圆的离心率是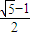 ,
,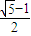 a,可得|AF|=c+a=(
a,可得|AF|=c+a=(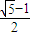 +1)a=
+1)a=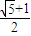 a.
a.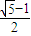 a2,
a2,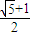 a2.
a2.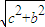 =a,
=a,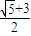 a2
a2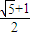 a)2=
a)2= a2
a2

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2007-2008学年山东省淄博七中高三(上)第二次月考数学试卷(理科)(解析版) 题型:选择题
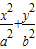 =1(a>b>0)的左准线上.过点P且方向为
=1(a>b>0)的左准线上.过点P且方向为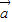 =(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )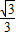

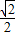

查看答案和解析>>
科目:高中数学 来源:《第2章 圆锥曲线与方程》2009年单元测试卷(宁波二中)(解析版) 题型:选择题
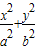 =1(a>b>0)的左准线上.过点P且方向为
=1(a>b>0)的左准线上.过点P且方向为 =(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )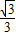

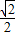

查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州二中高二(上)期末数学试卷(文科)(解析版) 题型:填空题
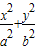 =1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .
=1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市江阴高级中学高三(上)10月学情调研数学试卷(解析版) 题型:解答题
 =1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .
=1(a>b>0)上,AB∥x轴,AD过左焦点F,则该椭圆的离心率为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com